1916번: 최소비용 구하기
첫째 줄에 도시의 개수 N(1 ≤ N ≤ 1,000)이 주어지고 둘째 줄에는 버스의 개수 M(1 ≤ M ≤ 100,000)이 주어진다. 그리고 셋째 줄부터 M+2줄까지 다음과 같은 버스의 정보가 주어진다. 먼저 처음에는 그
www.acmicpc.net
바로 이전 글인 1753번 문제 최단경로와 동일하게 다익스트라 알고리즘으로 해결 가능한 문제이다.
BOJ 1753번 최단경로
1753번: 최단경로 첫째 줄에 정점의 개수 V와 간선의 개수 E가 주어진다. (1 ≤ V ≤ 20,000, 1 ≤ E ≤ 300,000) 모든 정점에는 1부터 V까지 번호가 매겨져 있다고 가정한다. 둘째 줄에는 시작 정점의 번호
dev-game-standalone.tistory.com
동일한 풀이를 갖는 문제를 연속으로 올린 이유는, 이전 글 말미에 적어둔 부분 때문이다.
이러한 다익스트라 알고리즘이 성립하는 이유는 이미 방문한 노드가 항상 최단거리로 갱신이 되기 때문이다.
마지막에 첨언한 최단거리로 갱신됨이 보장된다는 내용은 또 다른 다익스트라 문제를 풀 때 설명하여 상호 참조하도록 하겠다.
그러므로 이번 글에서는 다익스트라의 동작은 알고 있다고 전제를 깔고 왜 이미 방문한 노드 그룹이 항상 최단거리로 갱신이 되는지를 보임에 포인트를 두겠다.
다익스트라 알고리즘에 대하여 모른다면 위 링크를 타고 조회수를 1 올려달라 설명을 참고하면 된다.
설명의 목적이 1916번 문제를 푸는 게 아니므로 문제에서 주어진 예시와 관련 없는 오른쪽과 같은(=임의의 그래프)를 만들어서 설명을 진행한다.
문제는 그냥 다익스트라만 구현하면 정답이 나올 수밖에 없다.
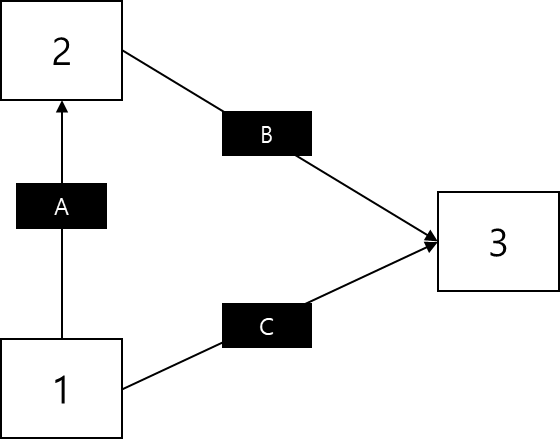
아래와 같은 그래프가 있다고 가정해보자. 대신 각 간선의 가중치는 미지수이다.

1번 노드에서 3번 노드로 이동해야 한다고 가정했을 때, 만약 C의 가중치가 A보다 작다면 A+B의 경로가 C보다 작을 수는 없다. (다익스트라는 모든 가중치가 양수 영역에서만 동작함을 기억하자)

만약 A와 C의 가중치가 같더라도 A+B의 경로의 가중치는 항상 C보다 크거나 같을 수밖에 없기 때문에, 3번 노드로 이동하고자 할 때 C의 가중치가 A의 가중치 이하라면 C를 선택하는 것이 무조건 옳다.
이번에는 반대로 A의 가중치가 C 보다 작다고 가정해보자. 그렇다면 A+B의 가중치가 C보다 작을 가능성이 존재한다.

이경우 2번 노드에서 3번 노드로 연결된 간선의 값을 비교할 때 2번 노드의 가중치를 추가로 더해서 비교를 하기 때문에
C와 A+B 간의 직접 비교가 되어 3번 노드로 이동하는 최솟값을 선택할 수 있게 된다.
이렇게 3개의 노드를 이용했을 때, 다익스트라 알고리즘이 각 노드 간의 최소 비용을 계산해 줄 수 있는 예시를 보았다.
이 예시를 재귀적으로 확대한다면 이미 방문한 노드(초록색 노드)는 항상 최단거리 값을 가지고 있음을 확인할 수 있다.

1번 노드가 사실은 서로가 최단거리 탐색이 완료된 [가], [나], [다] 노드의 집합체였다고 가정해보자.
출발 노드는 [가] 노드이다.
그렇다면 1, 2, 3번 노드가 있던 그래프는 사실 아래와 같았던 것이다.

1번 노드에서 3번 노드로 이동하는 최소비용 문제는 [가] 노드에서 [3] 노드로 가는 최소비용 문제로 바뀌었다.
1->2->3
1->3
이지선다 문제에서
가 -> 다 -> 3
가 -> 나 -> 다 -> 3
가 -> 나 -> 2-> 3
가 -> 다 -> 나 -> 2 -> 3
경로가 2배로 증가했다.
하지만 다시 생각해보면 [가], [나], [다] 노드는 탐색이 완료된 노드들이다. 즉 [다] 노드에는 이미 [가]->[나]->[다]가 적합한지, [가]->[다]가 적합한지 비교가 된 채로 최소 가중치가 이미 들어 있는 것이다.

즉 4개인 줄 알았던 경로는 1이 이미 탐색되었기 때문에 아래와 같이 2개로 좁혀서 해결이 가능하고
(가 -> 다) -> 3
(가 -> 나 -> 다) -> 3
(가 -> 나) -> 2-> 3
(가 -> 다 -> 나) -> 2 -> 3

이는 1, 2, 3 만 있던 최초의 문제와 동일한 문제가 된다

즉 탐색된 그룹에서 외부로 연결된 간선들의 최솟값을 이용해서 계속 탐색해 나간다면 새롭게 탐색되는 노드의 가중치는 시작 지점부터의 최소 가중치임을 보장할 수 있고, 이를 반복하여 그래프 전체에 대한 최소 비용을 계산할 수 있게 되는 것이다.
code
GitHub - YoungWoo93/algorithmOnlineJudge: 알고리즘 온라인 저지
알고리즘 온라인 저지. Contribute to YoungWoo93/algorithmOnlineJudge development by creating an account on GitHub.
github.com
뭔가 당연하다고 생각했던 부분을 글로 적으려 하니 생각보다 어려웠다.
이렇게 설명하는 게 맞는지도 모르겠다.
하지만 내가 알고 있는 그대로를 적어 두는 것도 의미가 있겠다 싶어서 우선은 적었고 아마 조만간 풀 벨만 포드 알고리즘 문제를 포스팅할 때 다른 분들이 적은 다익스트라 설명글을 좀 참고해서 글을 다듬어야겠다.
'알고리즘 온라인 저지 > BOJ' 카테고리의 다른 글
| BOJ 1202번 보석 도둑 (0) | 2022.01.18 |
|---|---|
| BOJ 2014 소수의 곱 (0) | 2022.01.18 |
| BOJ 1697번 숨바꼭질 (0) | 2022.01.12 |
| BOJ 1002번 터렛 (0) | 2022.01.11 |
| BOJ 1753번 최단경로 (0) | 2022.01.11 |



