1753번: 최단경로
첫째 줄에 정점의 개수 V와 간선의 개수 E가 주어진다. (1 ≤ V ≤ 20,000, 1 ≤ E ≤ 300,000) 모든 정점에는 1부터 V까지 번호가 매겨져 있다고 가정한다. 둘째 줄에는 시작 정점의 번호 K(1 ≤ K ≤ V)가
www.acmicpc.net
그래프의 간선에 가중치가 존재할 때, 최소 / 최대 비용을 구하는 알고리즘 중 하나인 다익스트라(Dijkstra) 알고리즘을 아는지 묻는 문제이다. 다만 다익스트라 알고리즘은 간선의 가중치가 양수 영역에 있어야 한다. 음수 가중치를 가지는 그래프의 최단거리 탐색 문제는 벨만 포드 알고리즘을 이용하도록 하자.
벨만 포드 알고리즘 문제도 조만간 하나 풀어야겠다.
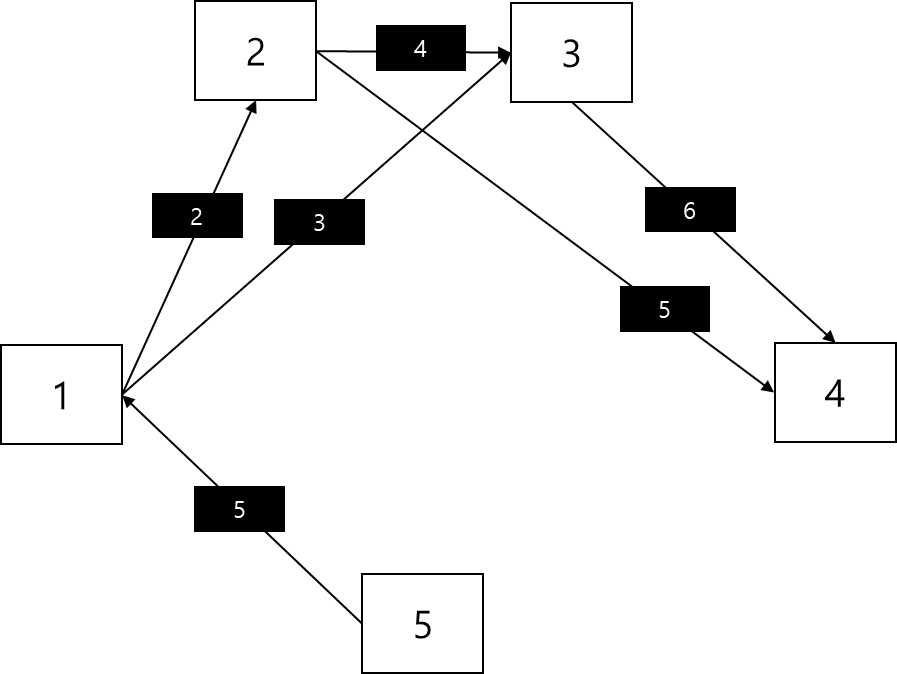
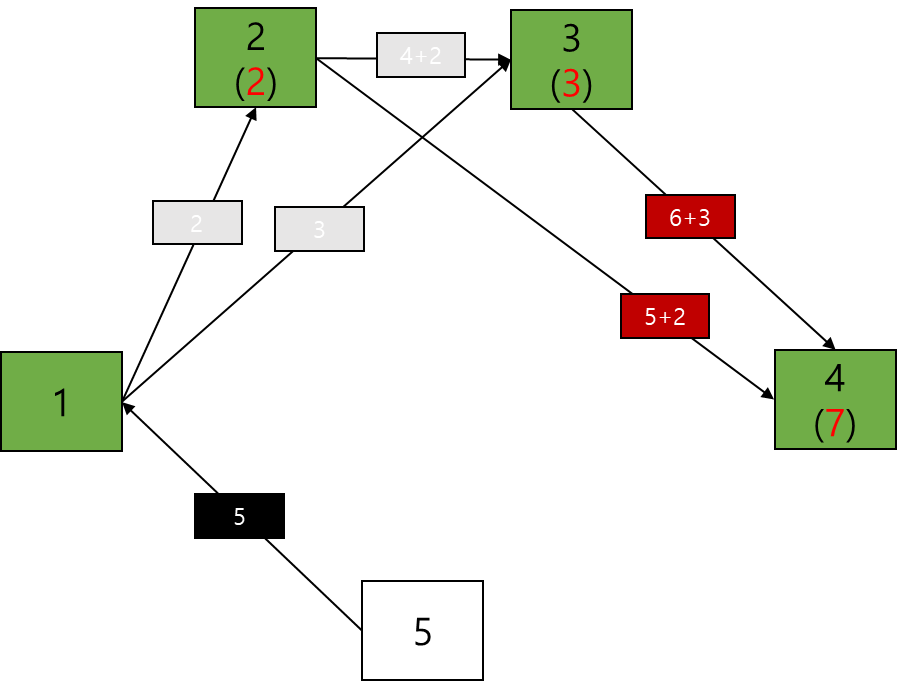
문제의 예시를 그래프로 나타내면 오른쪽과 같다.
커다란 블록은 노드를 의미하고, 화살표는 간선, 작은 블록은 간선의 가중치(비용)를 의미한다. 이 문제에서의 가중치는 거리이다.
이 그래프를 이용하여 다익스트라 알고리즘의 동작을 설명하고자 한다.
먼저 이 문제에 정답을 띄우기 위해서는 우선순위 큐를 같이 이용해야 한다. 하지만 다익스트라 자체는 우선순위 큐와 상관이 없는 알고리즘이다. (우선순위 큐 를 이용하여 시간 복잡도를 줄일 수 있을 뿐이다) 그러므로 순수한 다익스트라 알고리즘 자체를 설명하는데 포스팅 목표를 둔다.
다익스트라 알고리즘의 규칙은 다음과 같다.
- (규칙 A) "이미 방문한 노드" 들의 간선중 가장 적합한 비용을 가지는 간선을 탐색한다. (ex : 최소비용을 구하는 문제라면 가장 작은 값, 최대 비용을 구하는 문제라면 가장 큰 값)
- (규칙 A-1) 이때, 간선의 비용은 (해당 간선의 가중치 + 해당 간선이 출발하는 노드까지의 비용)으로 계산한다.
- (규칙 B) 규칙 A에 의해 도착한 노드가 "방문한 적이 없는 노드"인 경우, 해당 간선의 비용이 도착한 노드까지의 비용으로서 저장된다.
- (규칙 C) 규칙 A에 의해 도착한 노드가 "이미 방문한 노드"인 경우, 미리 저장된 비용과 해당 간선의 비용 중 더 적합한 값을 저장한다. (ex : 최소비용을 구하는 문제라면 작은 값, 최대 비용을 구하는 문제라면 최댓값)
- (규칙 D) 규칙 B, 또는 C에서 이용한 간선은 더 이상 참조하지 않는다.
- (규칙 E) 모든 간선이 소진될 때까지 규칙 A ~ D를 반복한다.
이 규칙 (= 알고리즘)에 따라서 1753번 문제의 예시를 풀어보자.

우선 시작점의 노드는 "방문한 노드"로 넣어주며 시작하게 된다. 예시의 경우 1번 노드에서 시작한다.
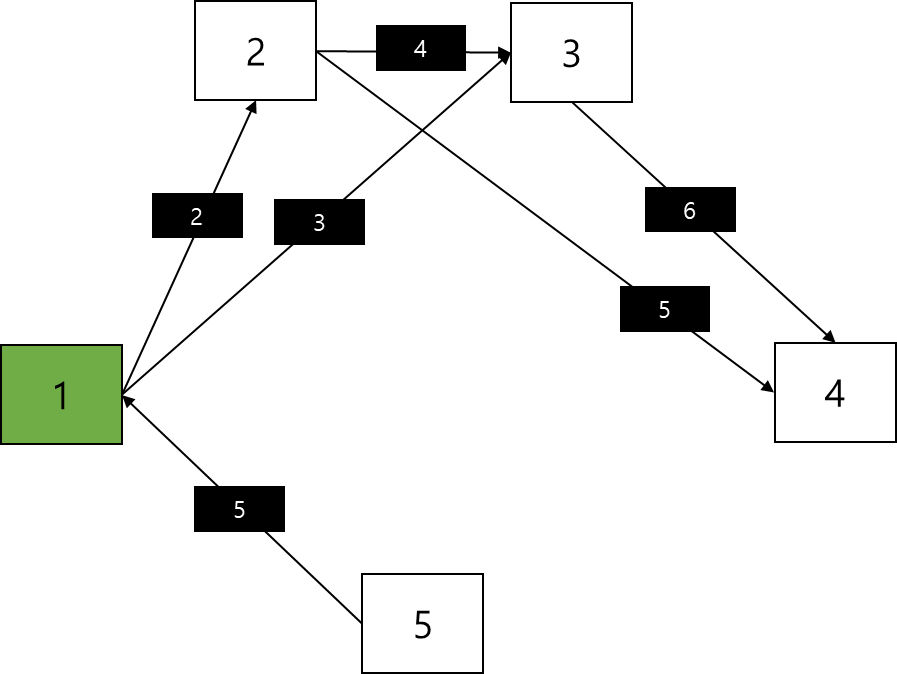
이후 규칙 A를 수행하기 위해 1번 노드의 간선들을 모두 리스트 등에 넣는다.

이후 규칙 A를 수행한다.

규칙 B에 의해 2번 노드가 "방문한 노드"로 바뀌었고, 간선의 비용인 2가 2번 노드에 저장된다.

규칙 D에 의해 1번 노드에서 2번 노드로 가는 가중치 2 간선은 참조되지 않는다. (삭제)

규칙 A를 다시 적용한다. 이때, 규칙 A-1에 의해 2번 노드에서 3, 4번 노드로 가는 가중치 4, 5 간선은 2번 노드의 비용인 2를 더하여 6, 7로서 계산된다.



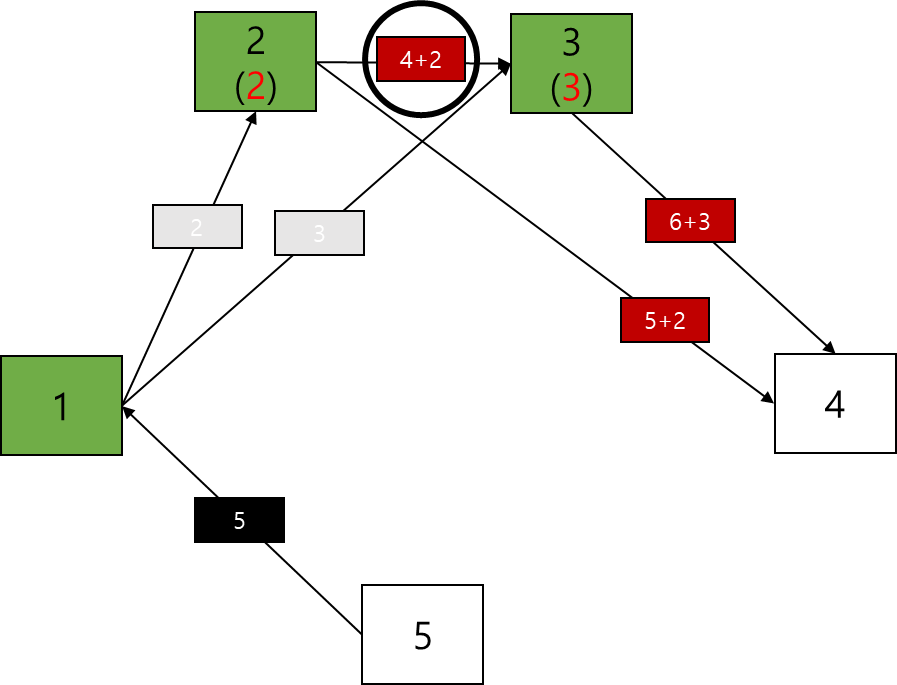
이 단계에서 남아있는 간선들 중 최소 값인 6 간선으로 3번 노드를 갱신할 수 없다 (규칙 C)
이경우 그대로 비활성화시키고 계속 진행하면 된다.
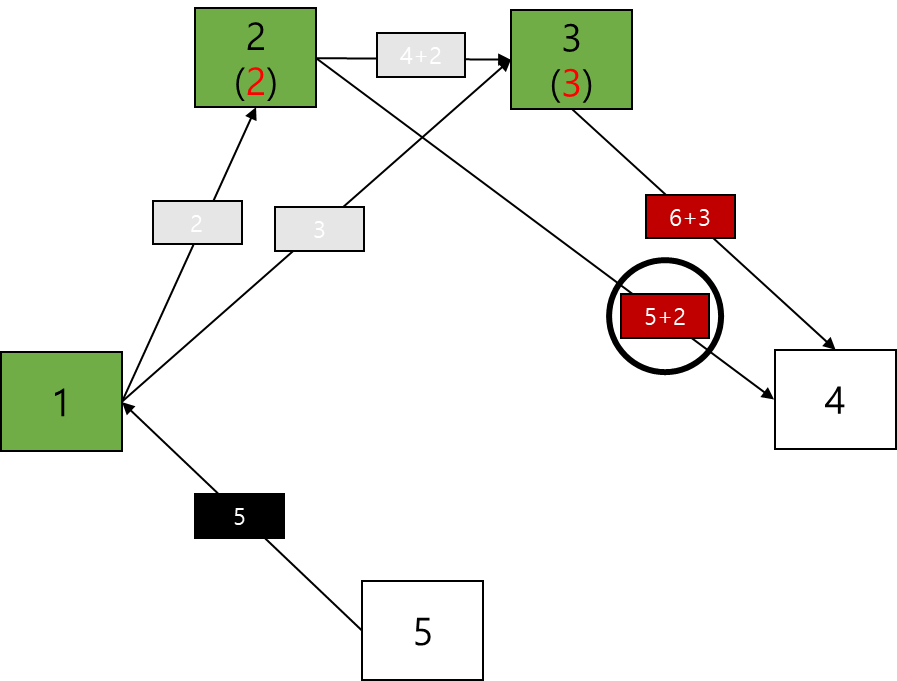


간선을 저장한 리스트가 모두 비었음에도 (=붉은 간선이 더 이상 남아있지 않음에도) 5번 노드는 탐색이 불가능했다.
탐색이 불가능한 노드는, 출발 노드부터 탐색 불가 노드까지의 경로가 없다고 판정하면 된다.
즉 이 단계까지 오면 1번 노드에서 각 노드까지의 최단거리가 확정된다.
1->1 : 0
1->2 : 2
1->3 : 3
1->4 : 7
1->5 : INF
이러한 다익스트라 알고리즘이 성립하는 이유는 이미 방문한 노드가 항상 최단거리로 갱신이 되기 때문이다.
참고:
BOJ 1916 최소비용 구하기
1916번: 최소비용 구하기 첫째 줄에 도시의 개수 N(1 ≤ N ≤ 1,000)이 주어지고 둘째 줄에는 버스의 개수 M(1 ≤ M ≤ 100,000)이 주어진다. 그리고 셋째 줄부터 M+2줄까지 다음과 같은 버스의 정보가 주
dev-game-standalone.tistory.com
code
GitHub - YoungWoo93/algorithmOnlineJudge: 알고리즘 온라인 저지
알고리즘 온라인 저지. Contribute to YoungWoo93/algorithmOnlineJudge development by creating an account on GitHub.
github.com
백준 1753번 문제에서는 간선들의 최솟값을 찾을 때 우선순위 큐 를 이용하여 찾는다면 정답을 받을 수 있을 것이다.
마지막에 첨언한 최단거리로 갱신됨이 보장된다는 내용은 또 다른 다익스트라 문제를 풀 때 설명하여 상호 참조하도록 하겠다. 참조 완.
추가로 다익스트라가 음수 영역에서 동작하지 않는 내용은 벨만 포드 알고리즘 문제를 풀 때 설명하도록 하겠다.
'알고리즘 온라인 저지 > BOJ' 카테고리의 다른 글
| BOJ 1697번 숨바꼭질 (0) | 2022.01.12 |
|---|---|
| BOJ 1002번 터렛 (0) | 2022.01.11 |
| BOJ 1644 소수의 연속합 (0) | 2022.01.10 |
| BOJ 4948 베르트랑 공준 (0) | 2022.01.10 |
| BOJ 1715번 카드 정렬하기 (0) | 2022.01.09 |



