자료구조 개념 : 레드 블랙 트리 (Red Black Tree, RB tree)
레드 블랙 트리는 일반 이진트리에서 자식들이 한쪽으로 치우치는 것을 막기 위한 균형 기능이 추가된 트리이다. 이를 자가 균형 이진트리(Self-balancing binary tree)라 부른다. 자가 균형 이진트리
dev-game-standalone.tistory.com
이전 포스팅에서 RB 트리의 4가지 조건을 알아보았다.
이 4가지 규칙 중 삽입과 삭제에서 핵심이 되는 규칙은
- 모든 red는 black 자식을 갖는다. (= red가 red의 부모가 될 수 없다.)
- 임의의 노드에서 출발하는 모든 경로는 모두 같은 수의 black 노드가 존재한다.
두 가지가 있다. 이 두 가지를 유의하며 RB 트리의 삭제를 살펴보자.
우선 RB트리의 삭제는 삭제하고 싶은 노드를 찾고, 그 노드를 대체할 수 있는 노드 (이진 탐색 트리의 삭제와 동일하다)를 찾아 target으로 만드는 것부터 시작한다.
이후의 RB 트리의 삭제 규칙은 다음과 같다.
- 타겟 노드의 색이 red 일 경우 그대로 삭제한다.
- 타겟 노드의 색이 black일 경우 (= black 균형이 깨진 경우)
- 타겟 노드 쪽에 black을 1개 추가해준다.
- 타겟의 조카들이 모두 black 인경우 -> 부모의 색을 타겟과 타겟의 형제에게 나누어준다.
- 타겟의 조카중 일부가 red 인경우 -> 회전을 이용한다.
- 타겟 노드 쪽에 black을 1개 추가해준다.
- 마무리.
예시를 살펴보자.
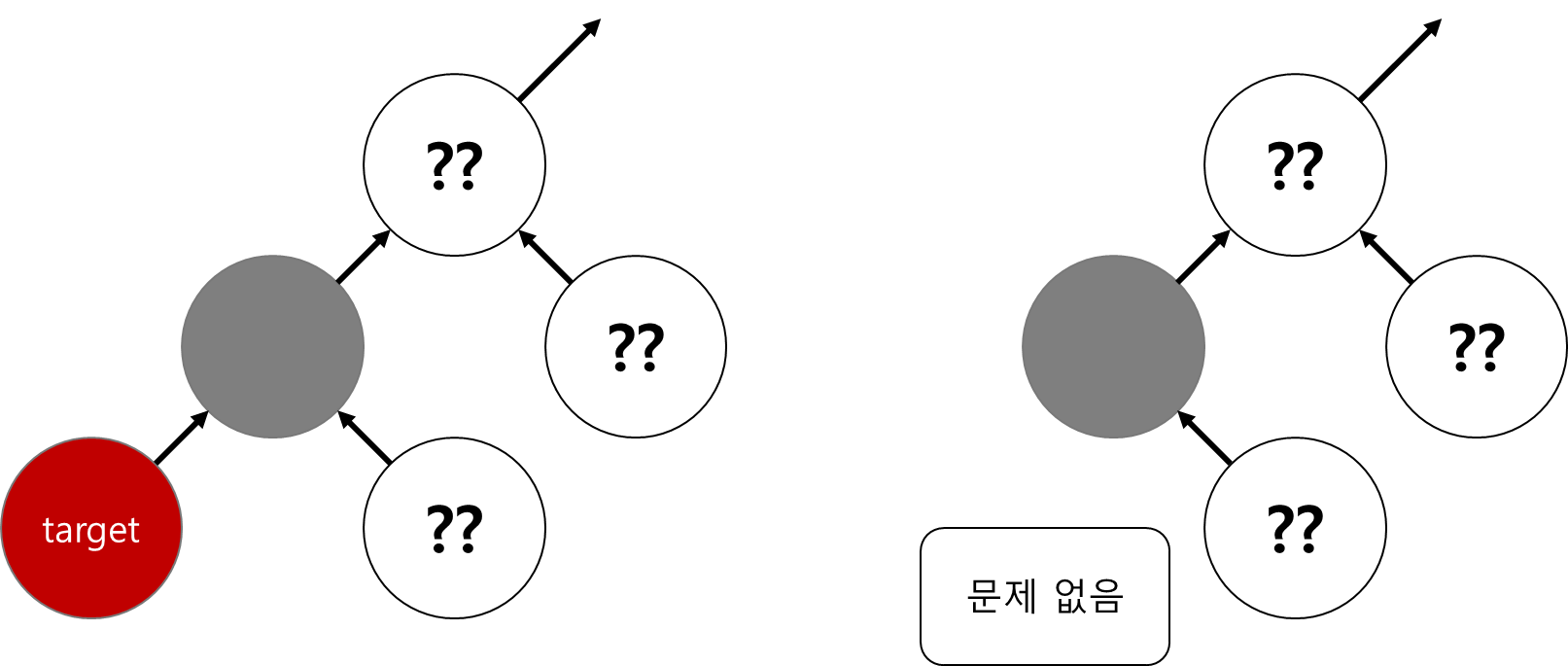
타겟 노드의 색이 red 일 경우 그대로 삭제한다.
target이 red라면 아무런 문제가 없다.
target이 red라는 것은 target의 부모는 black이라는 것이다.
red가 그냥 사라지더라도 red - red 문제는 발생하지 않으며, black은 변한 것이 없기 때문에 당연히 균형도 맞춰진 그대로이다.
타겟 노드의 색이 black일 경우
타겟 노드 쪽에 black을 하나 추가해준다.
타겟의 조카들이 모두 black 인경우 -> 부모의 red를 타겟과 타겟의 형제에게 나누어준다.
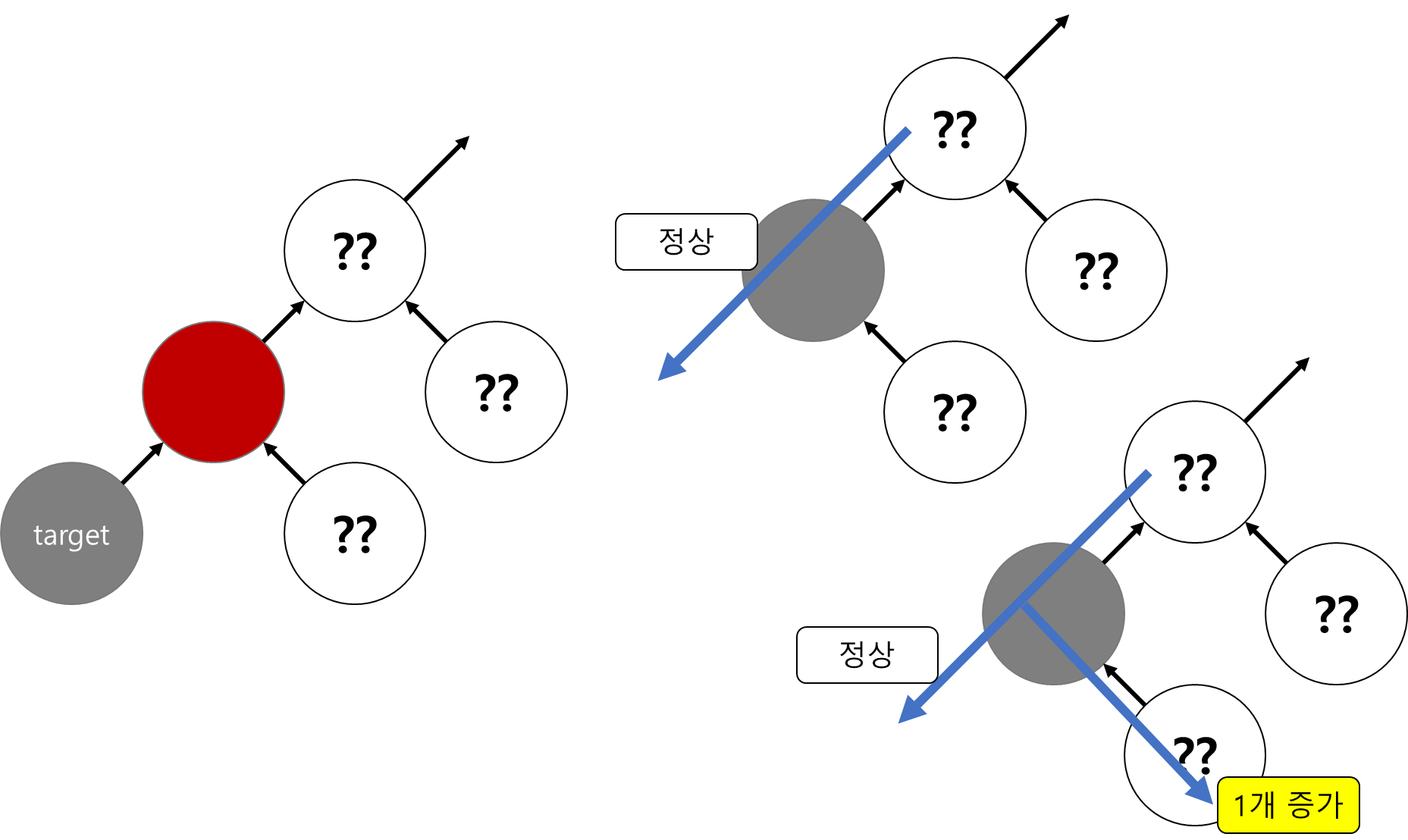
하지만 타겟이 black인 경우, 바로 해결하기엔 문제가 있다.
black을 그냥 삭제하면 해당 방향 black 노드의 개수가 1개 감소하여 균형이 깨진다.
만약 타겟의 부모가 red여서 부모로 black을 올려주고, 삭제한다고 하더라도
타겟의 형제 방향으로 black의 개수가 1개 증가하는 문제가 생긴다.
물론 타겟의 형제는 항상 black일 것이다. (타겟의 부모가 red 이므로)
그렇기 때문에 다음과 같이 가능한 경우도 존재한다.
이 경우 타겟의 색이 red로 바뀐 것과 동일하므로 red 타깃을 삭제하는 것처럼 타깃을 지우고 종료할 수 있다.
하지만 타겟의 형제의 자식 중 하나라도 red였다면, red - red 문제가 발생한다.
즉 단순한 방법으로는 불가능하고, 타겟 방향에 black을 하나 추가해주는 회전 동작이 필요하다.
타겟 노드의 색이 black일 경우
타겟 노드 쪽에 black을 하나 추가해준다.
타겟의 조카중 일부가 red 인경우 -> 회전을 이용한다.
우선 가능한 경우를 먼저 보자.
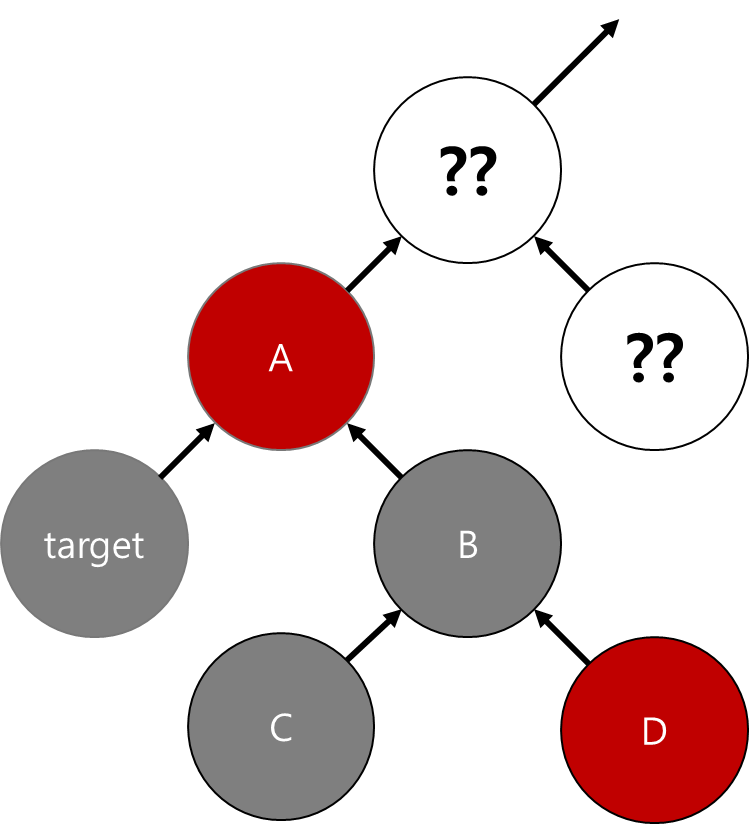
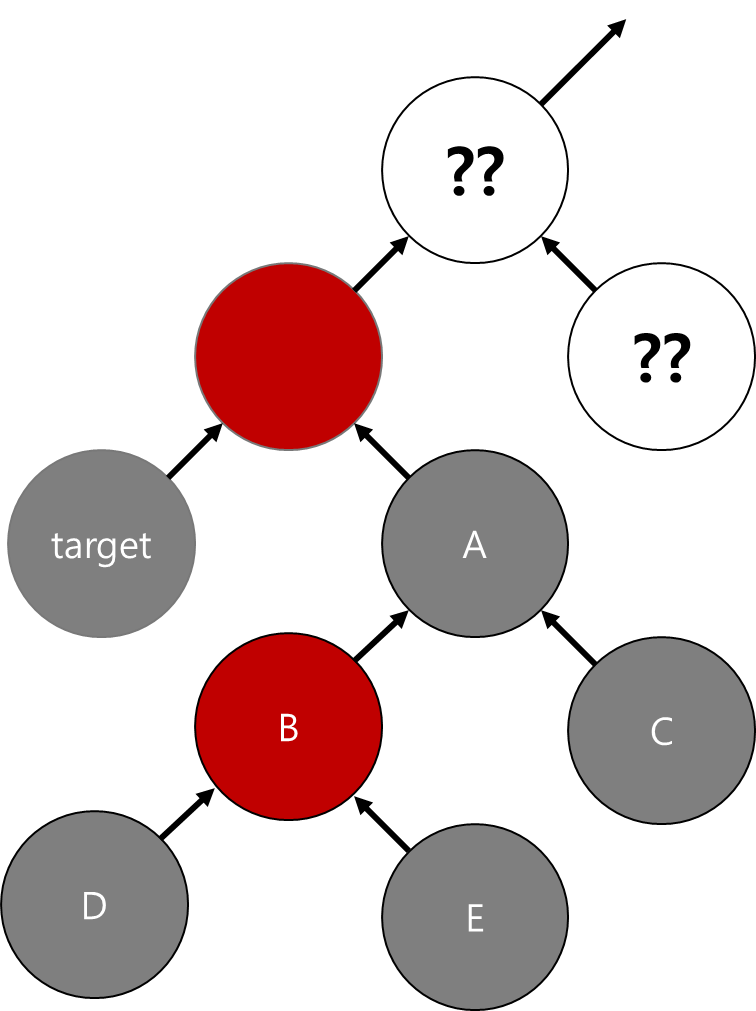
타겟의 조카 중, 타겟에 가까운 조카 (= C 노드)가 black인 경우에는
타겟의 부모 (= A 노드)를 기준으로 하는 타겟 방향 회전을 통해 해결이 가능하다.
회전 전후의 경로상 black을 확인해보면
타겟 방향의 black만 1개 추가되었다.
이제 다른 모든 경로에 비해 타겟 방향만 black이 1개 더 많은 상황이 됐으므로 black 타겟을 지움으로써 전체의 균형이 맞게 된다.
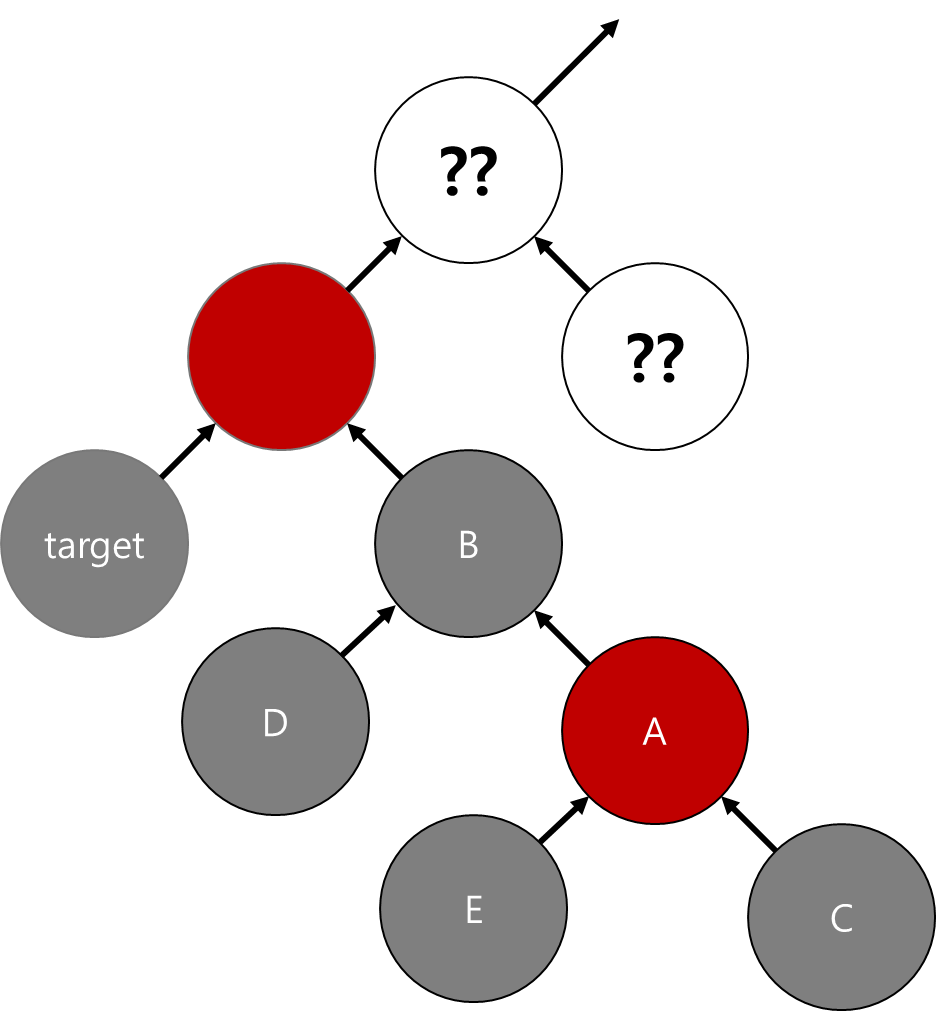
타겟의 조카 중, 타겟에 가까운 조카 (= C 노드)가 red인 경우에는 위와 동일한 방법을 사용할 경우 red - red 문제가 발생한다.
이때 A와 D가 모두 red 라면 다음과 같이 red를 올려주는 방법이 가능하다.
즉 타겟의 조카가 둘 다 black이거나
타겟의 조카중 타겟에서 먼 조카가 red 인경우 해결이 가능하다.

이제 아래의 형태만 해결할 수 있으면 모든 경우에 대하여 가능하다.
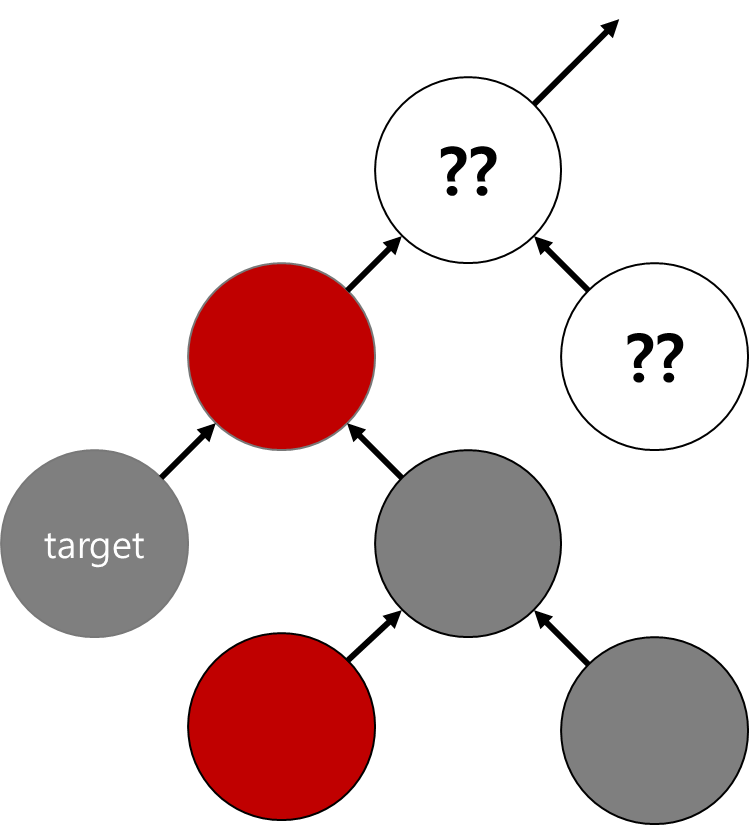
이 문제를 해결할 때 RB 트리의 규칙 중 모든 NIL 노드를 블랙으로 간주한다는 규칙이 힘을 발휘한다.
물론 NIL = black 규칙이 없더라도 불가능하지는 않다. 다만 많은 예외처리가 필요하다.
NIL 노드 규칙을 이용해 해결하는 것을 보자.
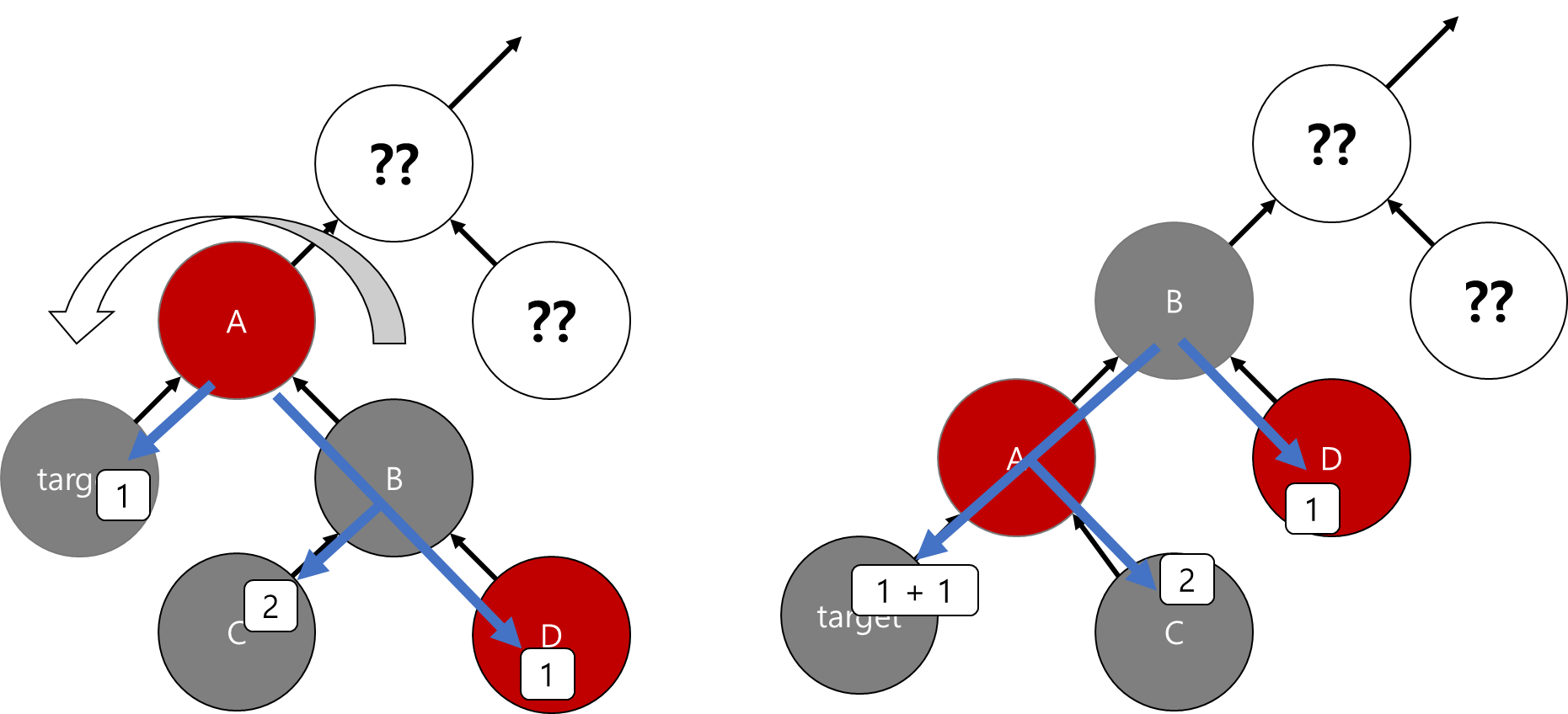
타겟의 가까운 red 조카 (B 노드)는 확정적으로 black 2개를 자식으로 가지고 있다.
그것이 실제 값을 가진 노드일 수도 있고, NIL 노드 일 수 도 있지만 여하튼 black 2개를 확정적으로 갖는 점을 이용하자.
타겟의 형제를 기준으로 타겟에 먼 방향으로 회전을 하면 red - red 문제와 black 개수 문제가 발생한다.
이를 동시에 해결할 수 있다.
B를 black으로 바꾸어 red red 문제와 B, D의 black -1 문제를 동시에 해결한다.
이제 A에서 시작하는 서브트리의 black + 1 문제를 해결하기 위해 A를 red로 바꾸어준다.
이렇게 타겟의 형제 기준 회전을 마무리한다.
타겟의 형제 기준 회전을 끝내고 보면, 어느새 트리는 해결 가능한 모양이 되어있다.
정확히는 회전을 했더니 해결 가능해진 것이 아니라, 해결 가능한 모양이 되도록 회전을 한 것이다. (형제를 타겟에서 먼 방향으로 회전시키기)
해결 가능한 꼴이 되었으니 위에서 한번 언급한 대로 타겟의 부모 기준, 타겟방향 회전을 한다.
그러면 타겟방향을 제외한 모든 경로는 동일한 black 개수를 갖게 되고, 타겟 방향은 black의 개수가 1 늘어났다.
이제 타겟을 삭제하면 black 개수 벨런스가 맞게 된다.
마무리.
이대로 끝은 아니다. 위의 D, E 노드는 NIL 노드일 수도 있고, 아닐 수도 있는 모호한 상태이다.
근데 NIL이든, 값이 있는 진짜 노드든 상관이 있을까?
NIL이었다면 그대로 지워서 안 보이게 하면 되는 것이고, NIL이 아니었다면 지금 상태가 맞는 상태이다.
추가로 지금 삭제에서 타겟의 부모를 모두 red로 가정했다.
부모가 black일 경우 부모를 기준으로 회전하는 단계에서, 먼쪽 조카의 black 개수가 1 줄어드는 문제가 발생할 수 있다.
이 경우에도 black의 갯수를 맞추는 단계에서 예외 처리가 가능하다.
RB 트리의 삽입, 삭제 방법은 한 가지가 아니다, 첫 포스트에서도 적었듯 RB 트리의 규칙만 만족한다면 어떤 방법을 이용하던 효율의 차이는 있을지언정 RB 트리가 맞다.
RB트리를 복습하는 과정에서 블로그나 위키 자료를 같이 참고했지만, 개인적으로 이중 흑색 노드를 이용하는 방법은 바로 이해가 안 됐었다. 그보다는 black이 1개 줄어드는 상황이므로 반대쪽에서 블랙을 하나 당겨온다는 개념이 이해하기 좋았고 그 방법을 설명해 보았다.
하지만 구현 자체는 마무리 단계에서 언급한 내용들을 직접 예외처리하는 것보다는 널리 알려진 방법을 이용하는 것이 편하다는 생각을 했다.
RB트리의 이해를 돕는 목적의 포스팅 이었으므로 색의 전파와 회전을 이용해 균형을 잡는 느낌이 전달되었으면 좋겠다.
(삭제 코드는 양이 조금 되기 때문에 질문사항은 댓글을 통해 문의 바랍니다.)
code :
GitHub - YoungWoo93/algorithm_online_judge_lib: 알고리즘 온라인 저지용 라이브러리
알고리즘 온라인 저지용 라이브러리. Contribute to YoungWoo93/algorithm_online_judge_lib development by creating an account on GitHub.
github.com
'알고리즘 온라인 저지 > 알고리즘 | 자료구조' 카테고리의 다른 글
| 자료구조 구현 : 레드 블랙 트리 (Red Black Tree, RB tree) - 삽입 (1) | 2022.09.08 |
|---|---|
| 자료구조 개념 : 레드 블랙 트리 (Red Black Tree, RB tree) (0) | 2022.09.01 |
| 자료구조 개념 : 우선순위 큐 (Priority Queue) + 힙 (Heap) (0) | 2022.08.25 |
| 자료구조 덱(deque, dequeue) (0) | 2022.08.15 |
| 알고리즘 : 탐욕법 (Greedy) (0) | 2022.08.11 |