자료구조 개념 : 레드 블랙 트리 (Red Black Tree, RB tree)
레드 블랙 트리는 일반 이진트리에서 자식들이 한쪽으로 치우치는 것을 막기 위한 균형 기능이 추가된 트리이다. 이를 자가 균형 이진트리(Self-balancing binary tree)라 부른다. 자가 균형 이진트리
dev-game-standalone.tistory.com
이전 포스팅에서 RB 트리의 4가지 조건을 알아보았다.
이 4가지 규칙 중 삽입과 삭제에서 핵심이 되는 규칙은
- 모든 red는 black 자식을 갖는다. (= red가 red의 부모가 될 수 없다.)
- 임의의 노드에서 출발하는 모든 경로는 모두 같은 수의 black 노드가 존재한다.
두 가지가 있다. 이 두 가지를 유의하며 RB 트리의 삽입을 살펴보자.
RB 트리의 삽입 규칙은 다음과 같다.
- 새로운 노드는 항상 red 노드로 추가한다.
- 만약 red - red 상황이 발생했다면, 삼촌의 색을 확인한다.
- 삼촌의 색이 red 라면 조부모에게 red를 모아서 올려준다.
- 삼촌의 색이 black 이라면 회전을 통해 해결한다.
예시를 살펴보자.
새로운 노드는 항상 red 노드로 추가한다.
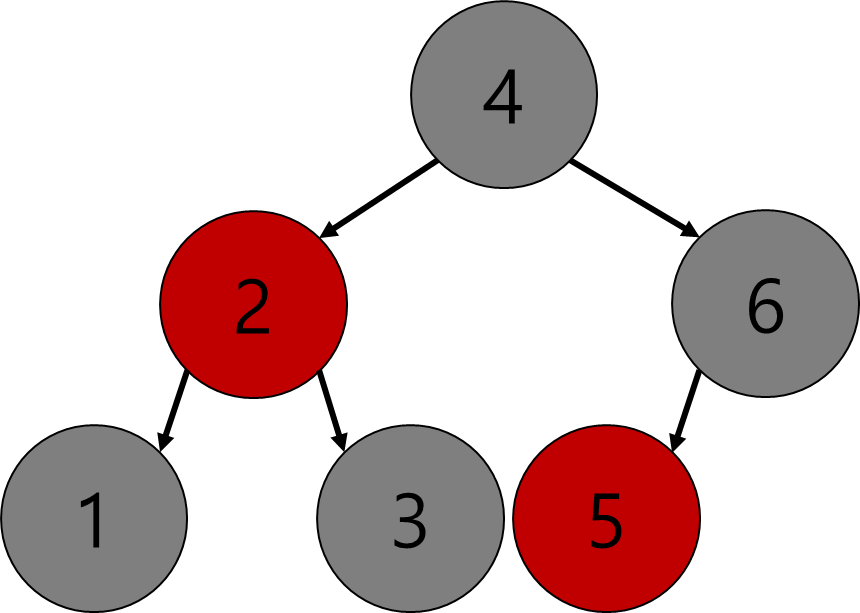
다음과 같은 RB 트리에 값이 0인 노드를 추가하려 한다.
이때, 0은 이진 탐색 트리의 규칙에 의해 1의 왼쪽 자식으로 추가되어야 한다.
그렇다면 0인 노드의 색은 어떤 색으로 추가되어야 할까?
만약 red로 추가된다면, 아무런 문제가 없다.
red - red 가 발생하지도 않았고, 루트에서 시작하는 모든 경로에 대하여 black이 2개로 동일하다.
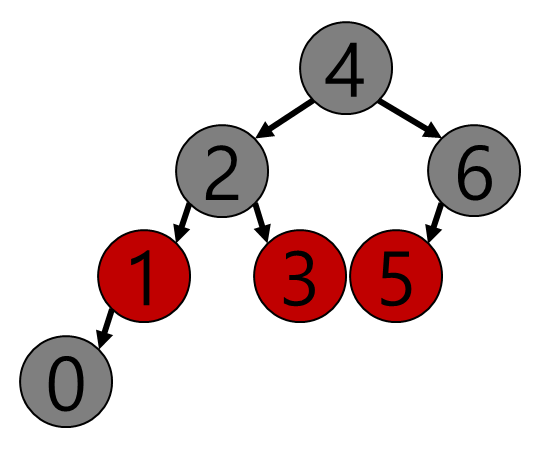
물론 0이 black으로 시작해도 불가능한 것 은 아니다.검은색 0이 삽입된 순간 루트에서 시작하는 모든 경로의 black 갯수가 깨져버렸다.
이를 맞추기 위해 red의 전파와 회전 동작을 통해 다 시 재 정렬을 할 수 있다.
삽입 노드를 red로 하던, black으로 하던 어떻게든 RB 트리의 모양을 만들 수 있다.
하지만 black을 삽입할 경우 100%의 확률로 트리의 균형이 깨지고, 재 균형 작업이 필요하다.
그에 비해 red를 삽입할 경우, 모든 경로의 black 개수 규칙에 영향을 받지 않기 때문에 삽입된 노드의 부모 색에 따라 균형이 깨지지 않는 경우가 존재한다.
100% 확률로 균형이 깨지는 상황과, 50% 확률로 균형이 깨지는 상황이라면 누구나 50% 확률을 고를 것이다.
그렇기 때문에 모든 삽입 노드는 red로 하기로 하자.
만약 red - red 상황이 발생했다면, 삼촌의 색을 확인한다
삼촌의 색이 red 라면 조부모에게 red를 모아서 올려준다.
삽입되는 노드를 red로 한정지 었다.
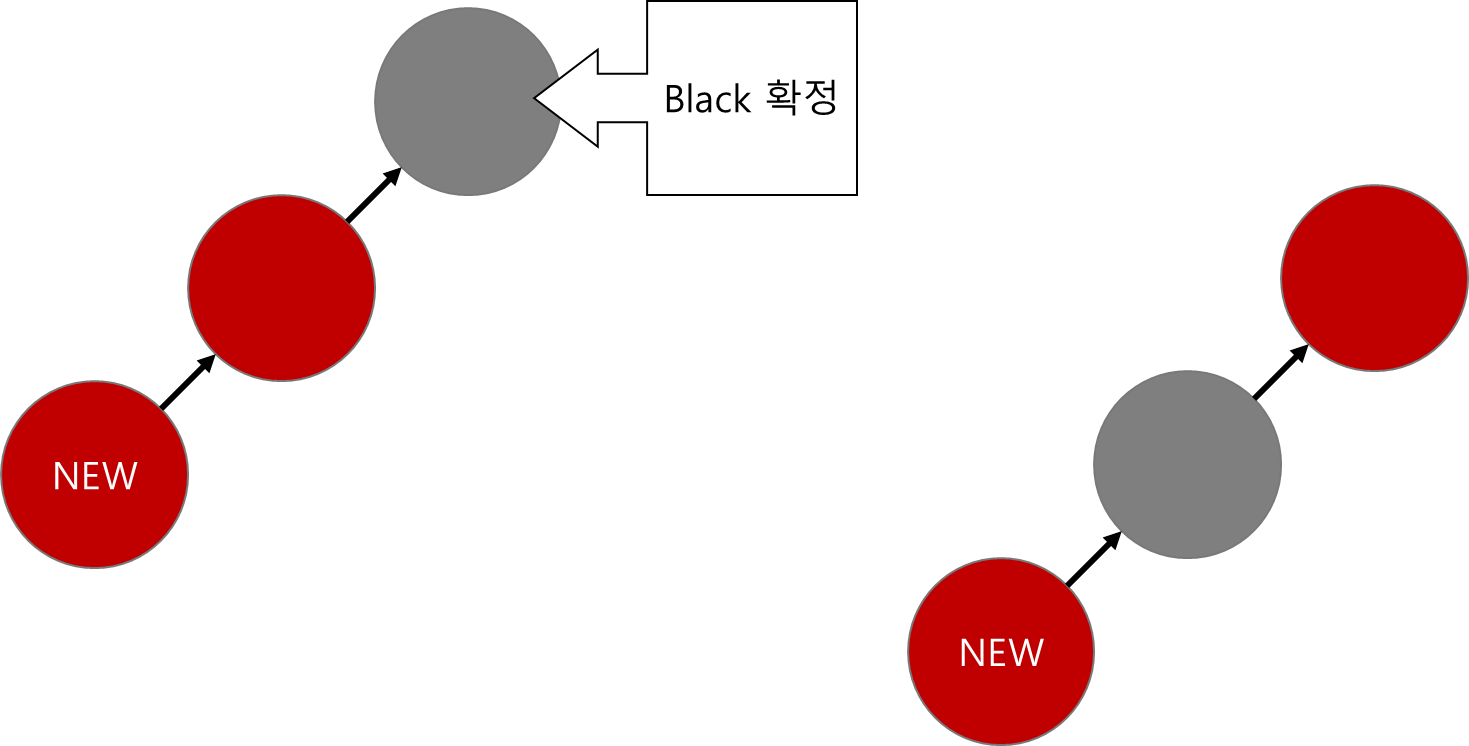
삽입되는 노드의 부모는 red이거나, black인 두 가지 경우가 존재한다.

만약 새로운 노드의 부모가 black이라면 아무런 문제가 없다. 그대로 삽입 동작이 종료되어도 된다.
하지만 새로운 노드의 부모가 red라면 red - red 문제가 발생한다.
이때, 어쩔 수 없이 부모나 새로운 노드의 색을 black으로 바꾸어 주어야 한다. 하지만 무턱대고 black으로 바꾼다면 black노드를 삽입할 때와 같이 전체적인 black 개수 균형이 깨지게 된다.
RB 트리에서는 이런 경우 red를 옮겨주는 개념을 이용해 균형을 최대한 유지한 채로 red - red 문제를 해결한다.
생각해보면 부모가 red라면, 부모의 부모, 즉 2칸 위의 노드는 항상 black 일 수밖에 없다.
왜냐하면 기존 트리가 RB 트리였기 때문에 red - red문제는 발생하지 않은 상태였을 것 이기 때문이다.
이렇게 되면 부모의 red를 위쪽으로 한 칸 밀어 올려서 red - red 문제를 해결할 수 있을 것 같다.
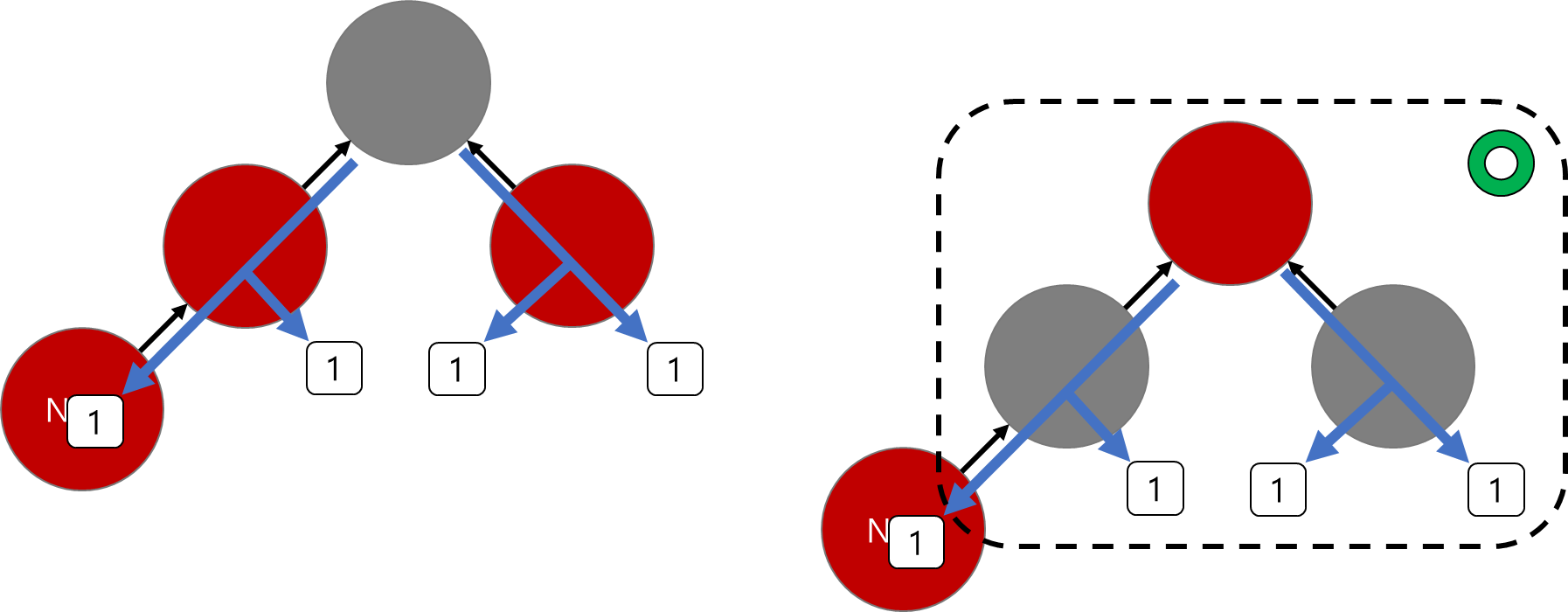
조금 더 자세한 상황을 보자.
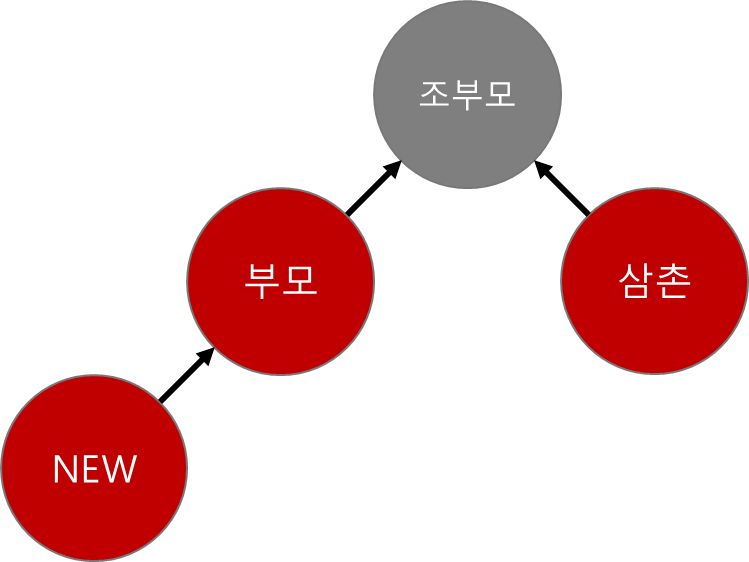
위와 같이, 자신의 부모와, 자신의 삼촌이 모두 red라면
이렇게 부모와 삼촌의 색을 모아 조부모에게 올려주는 느낌이라면 문제가 없을 것 같다.
red- red 문제도 없어졌을 뿐 아니라, 색을 옮기기 전과 옮긴 후의 모든 경로에 대해 black의 개수가 그대로 유지되었기 때문이다.
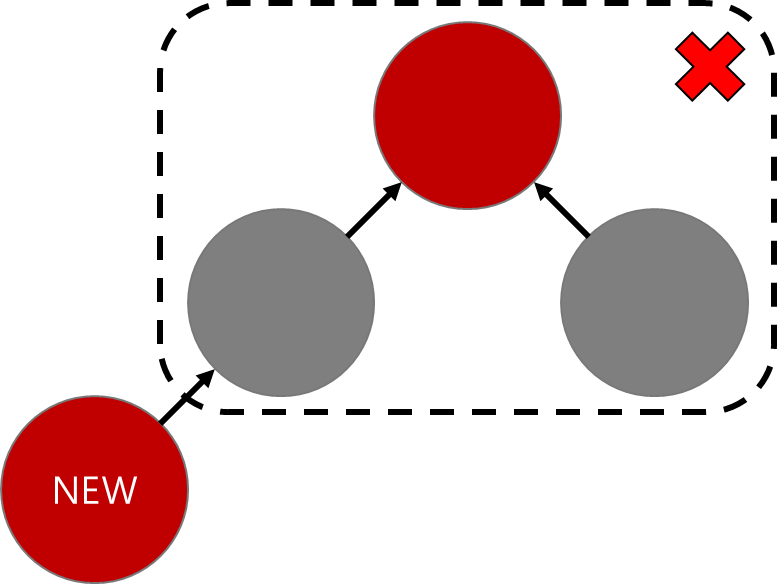
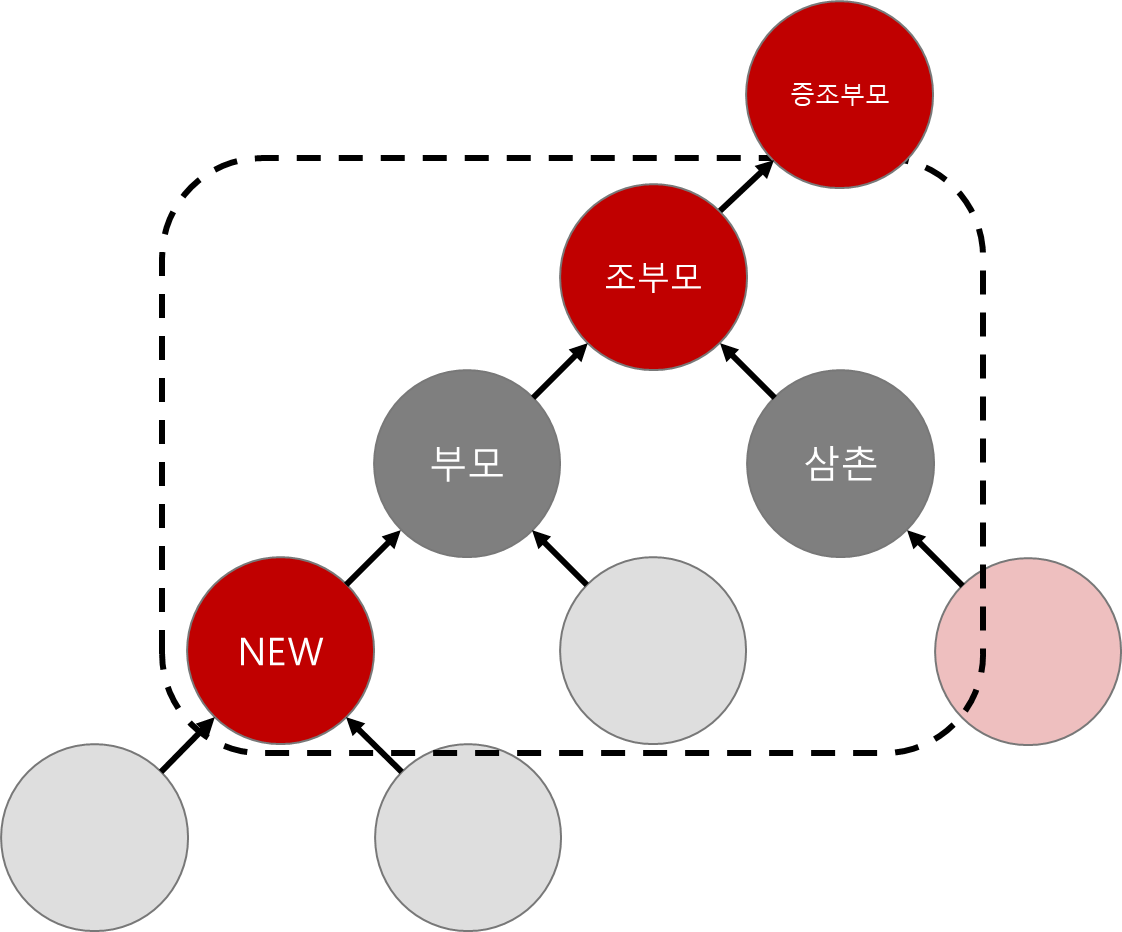
그렇다면 이번엔 삼촌의 색이 black인 경우를 보자.이경우 부모와 삼촌의 색을 모아서 올려준다는 느낌이 아니다.
부모의 색만 일방적으로 증조부에게 올려주게 된다.
색을 바꾸기 전과 후의 경로상 black의 개수를 보자.
원래 삼촌방향 black의 갯수는 2였는데, 부모의 색을 일방적으로 올렸을때엔 삼촌방향 경로의 black 갯수가 1 줄어들었다.
여기서 누군가는 "루트에서 시작한 모든 경로의 black 개수가 같아야 하는데, 오히려 삼촌 방향이 1로 맞춰져야 정상인 것 아닌가?" 라 고 생각할 수 있다.
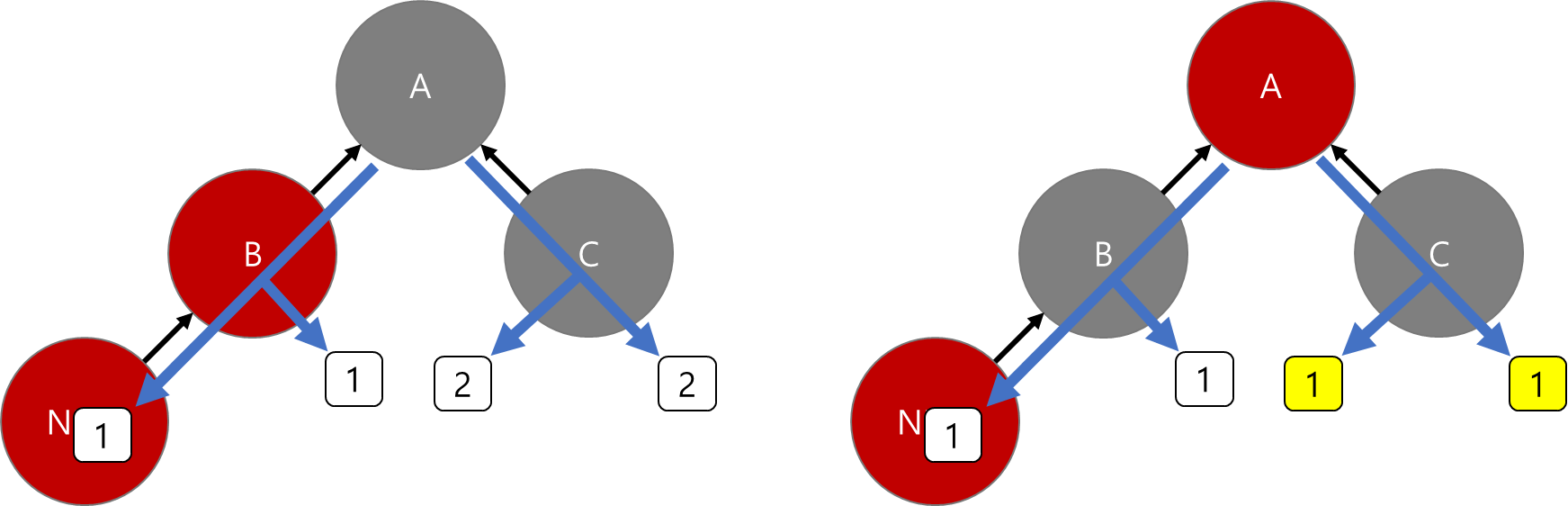
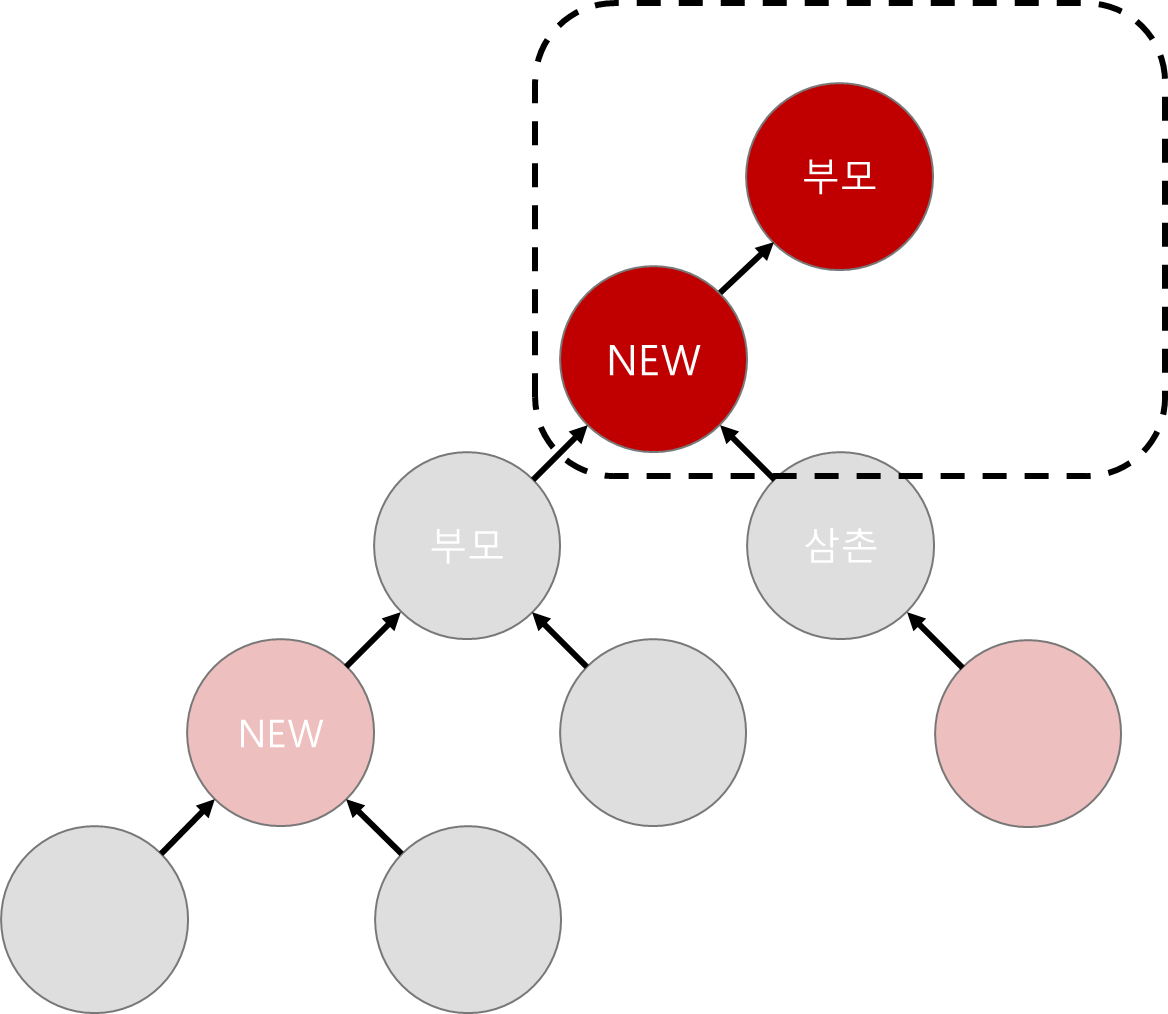
하지만 사실 전체 트리의 모양은 이러했고, 그중 우리가 관심 있는 부분만 강조해서 본 상황이었다.
그렇다면 당장 조부모에서 시작하여 삼촌까지는 black이 2개로 규칙이 어긋나 보이지만, 큰 그림에서는 오히려 규칙이 맞는 상황이었다.
RB 트리뿐만 아니라 재귀적으로 조건을 맞추는 시스템을 이해할 때엔 기존 상태는 균형이 맞아있는 상태라는 전제를 잊지 말아야 한다.
만약 red - red 상황이 발생했다면, 삼촌의 색을 확인한다
삼촌의 색이 black이라면 회전을 통해 해결한다.
삼촌 노드가 red였다면 부모와 삼촌의 red를 모아 조부모에게 올려주는 방법으로 해결할 수 있었지만.
삼촌 노드의 색이 black이라면 해당 방법이 불가능하다.
이때 RB 트리는 회전 개념을 이용하여 문제를 해결한다.
왼쪽 오른쪽의 black 개수가 맞지 않다면 회전을 이용해서 그 차이를 메꿔줄 수 있다.
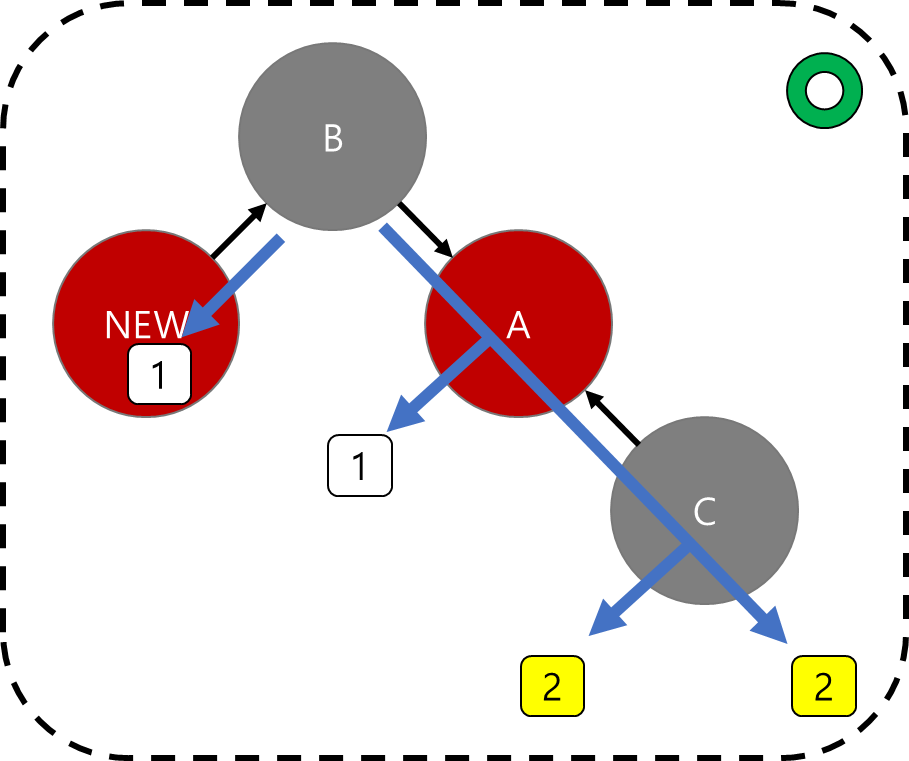
우선 삼촌의 색이 black임에도 조부모를 red로 만든 상황을 보자.
A의 입장에서 보면 오른쪽 자식 경로(C, 삼촌 경로)에 black을 한 개 더 주고 싶다.
오른쪽 자식 경로에만 black을 한 개 더 주는 방법은 왼쪽 자식을 자기 위치로 만들면 된다. 그렇게 하면 왼쪽 경로 블랙 +0, 오른쪽 경로 블랙 +1이 되기 때문이다.
잘 모르겠다면 위의 트리를 A를 기준으로 오른쪽으로 한 칸씩 회전시켜보자.
잘 모르겠다면, 자기가 red인 경우 오른쪽 서브 트리에 black을 1개 추가하고싶으면 우회전, 왼쪽 서브트리에 black을 1개 추가하고 싶다면 좌회전을 한다고 생각해도 된다.
하지만 회전 규칙이 성립하는 진짜 이유는
좌우의 공통조상을 black으로 만들어주어 양옆의 black을 1개씩 늘려줄 수 있다. + 좌측 또는 우측 서브 트리의 black을 한 개 감소시켜줄 수 있다 (회전을 통해) = 우회전을 하면 오른쪽만 black이 1개 추가된다. (좌회전은 왼쪽만 추가된다.)
라는 것을 한번 곰곰이 생각해보면 좋을 것이다.
이상의 규칙을 insert 함수를 보며 같이 살펴보자. (전체 코드는 맨 밑에 있다.)
RedBlackTreeNode<V>* insert(V value)
{
RedBlackTreeNode<V>* newNode = new RedBlackTreeNode<V>(value);
newNode->parent = nullNode;
newNode->left = nullNode;
newNode->right = nullNode;
newNode = insert(newNode);
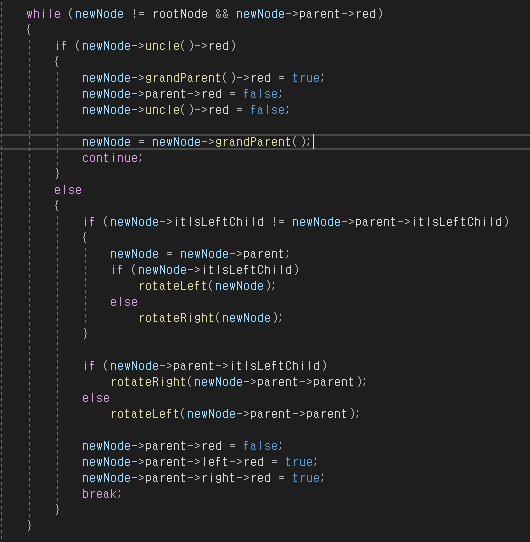
while (newNode != rootNode && newNode->parent->red)
{
if (newNode->uncle()->red)
{
newNode->grandParent()->red = true;
newNode->parent->red = false;
newNode->uncle()->red = false;
newNode = newNode->grandParent();
continue;
}
else
{
if (newNode->itIsLeftChild != newNode->parent->itIsLeftChild)
{
newNode = newNode->parent;
if (newNode->itIsLeftChild)
rotateLeft(newNode);
else
rotateRight(newNode);
}
if (newNode->parent->itIsLeftChild)
rotateRight(newNode->parent->parent);
else
rotateLeft(newNode->parent->parent);
newNode->parent->red = false;
newNode->parent->left->red = true;
newNode->parent->right->red = true;
break;
}
}
if (rootNode->red)
{
rootNode->red = false;
blackDepth++;
}
return newNode;
}
우선 newNode를 이진 탐색 트리 룰에 맞추어 삽입을 해준다.
그 이후 재귀적으로 규칙을 적용하며 올라가기 때문에 root 노드 체크와, 부모가 red인지를 체크한다.
만약 부모가 red가 아니라면 그대로 종료해도 된다.
여기서 root를 체크하는 이유가 이해되지 않는다면, 다음을 생각해보자.
"조부모를 red로 바꿨는데 증조부가 사실 red였다면?"
만약 삼촌이 red라면 간단하게 처리 가능하다.
그렇지 않다면 rotate 함수를 이용한다.
full code:
GitHub - YoungWoo93/algorithm_online_judge_lib: 알고리즘 온라인 저지용 라이브러리
알고리즘 온라인 저지용 라이브러리. Contribute to YoungWoo93/algorithm_online_judge_lib development by creating an account on GitHub.
github.com
'알고리즘 온라인 저지 > 알고리즘 | 자료구조' 카테고리의 다른 글
| 자료구조 구현 : 레드 블랙 트리 (Red Black Tree, RB tree) - 삭제 (0) | 2022.09.08 |
|---|---|
| 자료구조 개념 : 레드 블랙 트리 (Red Black Tree, RB tree) (0) | 2022.09.01 |
| 자료구조 개념 : 우선순위 큐 (Priority Queue) + 힙 (Heap) (0) | 2022.08.25 |
| 자료구조 덱(deque, dequeue) (0) | 2022.08.15 |
| 알고리즘 : 탐욕법 (Greedy) (0) | 2022.08.11 |