15711번: 환상의 짝꿍
환상의 나라 디디랜드에서는 인연의 증표로 끈을 하나씩 가지고 있다. 그들은 지극히 평범한 방법으로 이 끈을 이용하여 어떤 두 사람이 환상의 짝꿍인지 판단하는데, 두 사람의 끈을 서로 이
www.acmicpc.net
처음에는 그냥 소수를 구하는 문제라고 생각하여 에라토스테네스의 체 를 이용하여 풀이를 시도했다.
하지만 입력의 범위가 1012 범위이기 때문에 단순히 에라토스테네스의 체를 이용한다면 메모리 초과에 걸리게 된다.
결과적으로는 골드바흐의 추측을 추가로 이용하여 문제를 해결했다.
골드바흐의 추측 - 위키백과, 우리 모두의 백과사전
골드바흐의 추측(Goldbach's conjecture)은 오래전부터 알려진 정수론의 미해결 문제로, 2보다 큰 모든 짝수는 두 개의 소수(Prime number)의 합으로 표시할 수 있다는 것이다. 이때 하나의 소수를 두 번 사
ko.wikipedia.org
위키를 참조해보면 주어진 입력 범위에서 골드바흐의 추측을 이용한 문제 해결이 가능함을 알 수 있다.
컴퓨터로 직접 계산하여 짝수가 두 소수의 합인지 확인하는 시도가 예전부터 있었다. T. Oliveirae Silva는 1018
이하에서 골드바흐의 추측이 참임을 확인했다. 골드바흐의 추측은 반드시 두 소수의 합으로 표현하는 방법이 유일하다고 주장하는 것은 아니다. 소수 한 쌍의 합으로 표현하는 방법은 여러 가지가 있을 수 있고, 같은 두 수를 쓸 수도 있다.
우선 골드바흐의 추측을 이용해서 이번 문제를 풀 수 있는 이유를 설명한 뒤, 추측에 대한 간단한 설명과 해법을 적는다.
마지막으로 임의의 정수 N이 소수인지를 판별하는 방법에 대한 추가적 설명을 한다.
골드바흐의 추측은 짝수 추측과 홀수 추측으로 구성되어 있다.
4 이상의 임의의 짝수는 2개의 소수의 합으로 나타낼 수 있다 => 짝수 (강한) 추측
7 이상의 임의의 홀수는 3개의 소수의 합으로 나타낼 수 있다 => 홀수 (약한) 추측
위키로 이동해보면 2 초과의 짝수와, 5 초과의 정수로 나타나 있지만 사실상 위와 동일한 의미이다.
환상의 짝꿍 문제는 임의의 정수 두 개가 주어졌을 때, 그 합을 두 개의 소수로 나눌 수 있는가를 묻는 문제이므로 만약 주어진 두 정수의 합이 4 이상의 짝수라면 다른 계산 없이 바로 두 개의 소수로 나눌 수 있음을 알 수 있다. 이렇게 짝수는 추측을 이용하여 해결할 수 있지만 홀수는 어떻게 해결해야 할까? 사실 홀수 영역에 처리는 골드바흐의 추측과 상관없이 해결할 수 있다.
2를 제외한 모든 소수는 홀수이다.
임의의 홀수 2개를 더한 결과는 짝수이다.
=> 임의의 소수 2개를 더한 결과가 홀수가 되기 위해서는 임의의 소수중 한 개는 2일 수밖에 없다.
즉 문제에서 주어진 두개의 정수 합 S가 홀수라면 S-2 가 소수인 경우에만 환상의 짝꿍 관계가 될 수 있다.
환상의 짝꿍 문제를 다음과 같이 단순화할 수 있다.
- 입력으로 주어진 두 정수의 합 S가 4 이상의 짝수라면? => YES
- S가 홀수라면? => S-2 가 소수인지 체크
이상이 환상의 짝꿍 문제를 풀기 위한 아이디어이다.
추가로 임의의 정수 N이 홀수임을 확인하기 위한 방법으로 다음이 많이 추천된다.
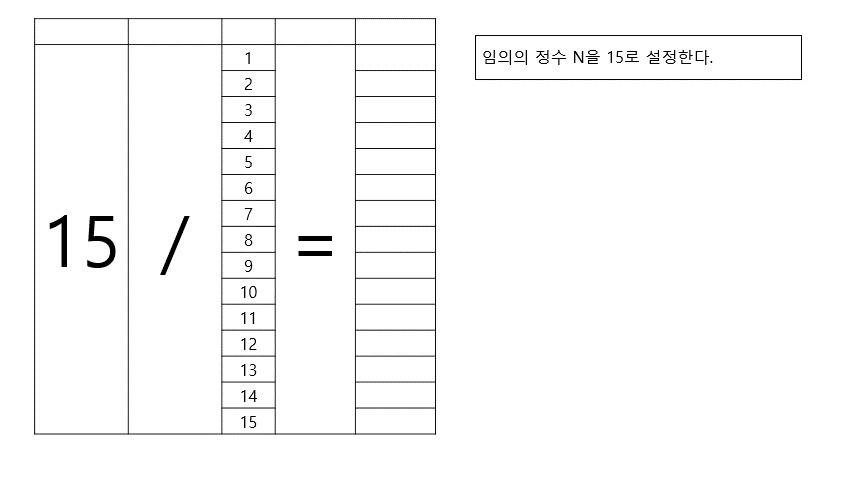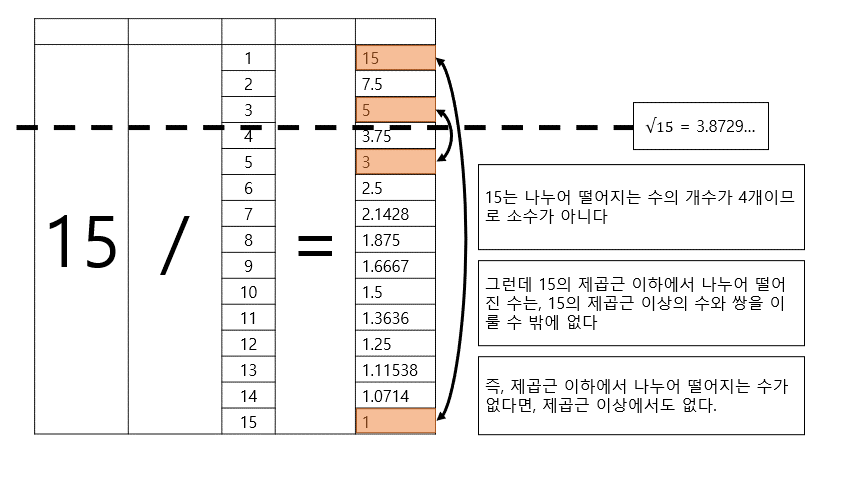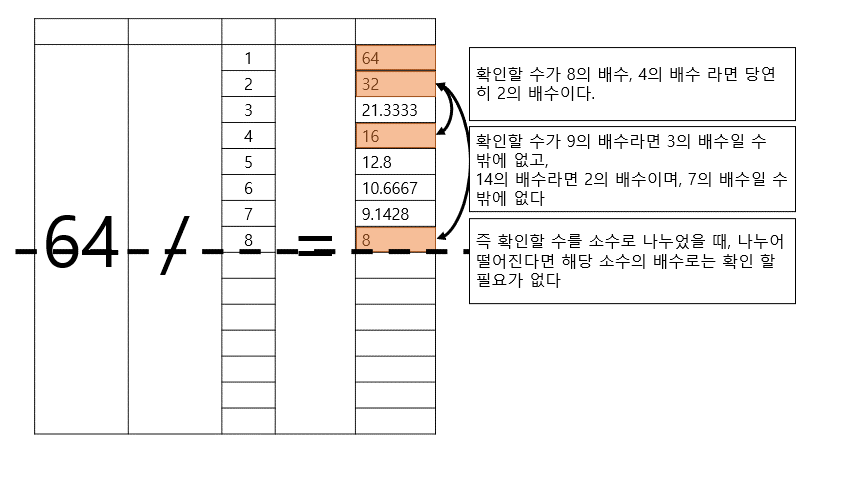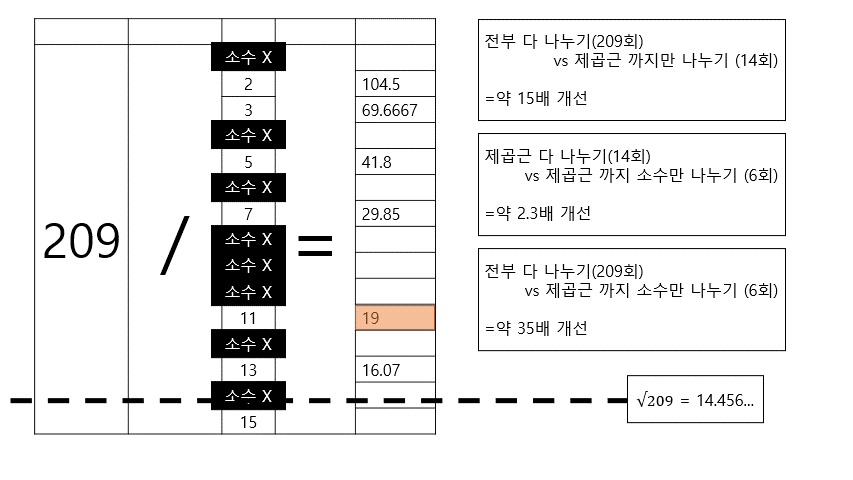
√ N 이하의 소수로 N를 나눈 결과, 나누어 떨어지는 것이 없으면 소수이다.
인터넷에서 너무나도 많이 추천되는 방법이고, 돌려보면 답이 나온다. 구현 또한 간단하다.
그래서인지 왜 N의 제곱근 이하까지만 구하면 되는지, 왜 소수로만 나누면 되는지 잘 모른 채 외운 사람들이 종종 있다.
그 부분에 대한 간단한 gif를 첨부한다.
code
GitHub - YoungWoo93/algorithmOnlineJudge: 알고리즘 온라인 저지
알고리즘 온라인 저지. Contribute to YoungWoo93/algorithmOnlineJudge development by creating an account on GitHub.
github.com
'알고리즘 온라인 저지 > BOJ' 카테고리의 다른 글
| BOJ 7579번 앱 (0) | 2022.06.24 |
|---|---|
| BOJ 2239번 스도쿠 (0) | 2022.06.24 |
| BOJ 11057번 오르막 수 (0) | 2022.05.12 |
| BOJ 1389번 케빈 베이컨의 6단계 법칙 (0) | 2022.05.12 |
| BOJ 7576 토마토 (0) | 2022.02.10 |

