11057번: 오르막 수
오르막 수는 수의 자리가 오름차순을 이루는 수를 말한다. 이때, 인접한 수가 같아도 오름차순으로 친다. 예를 들어, 2234와 3678, 11119는 오르막 수이지만, 2232, 3676, 91111은 오르막 수가 아니다. 수
www.acmicpc.net
그렇게 어렵지 않은 DP 문제이지만, 이러한 유형의 문제를 처음 푸는 입문자에겐 조금 어려울 수 있는 문제라고 생각한다.
규칙성만 파악할 수 있다면 문제의 해결 자체는 간단하기 때문에 규칙성 파악을 우선 해보자.

임의의 숫자 다음에 올 수 있는 숫자 (= 오르막 수 를 충족할 수 있는 숫자를)는 임의의 숫자보다 크거나, 같은 숫자만 올 수 있다.

즉 앞의 숫자가 1일 경우, 뒤에 올 수 있는 숫자는 1~9 사이의 값이며

앞의 숫자가 8 일 경우에는, 뒤에 올 수 있는 숫자는 8~9 사이의 값이다.
바로 위 상황을 하나의 블록으로 나타낸다면, 이 블록은 더 상위 블록에 일부일 수 있다는 것을 예측 가능하다.

이 내용을 정리하면
한자리 정수 S로 시작하는, N 자릿수의 양수 중 오르막 수의 개수를 climb(S, N)이라 표현한다면
climb(S, N) = climb(S+1, N) + climb(S, N-1)이다.
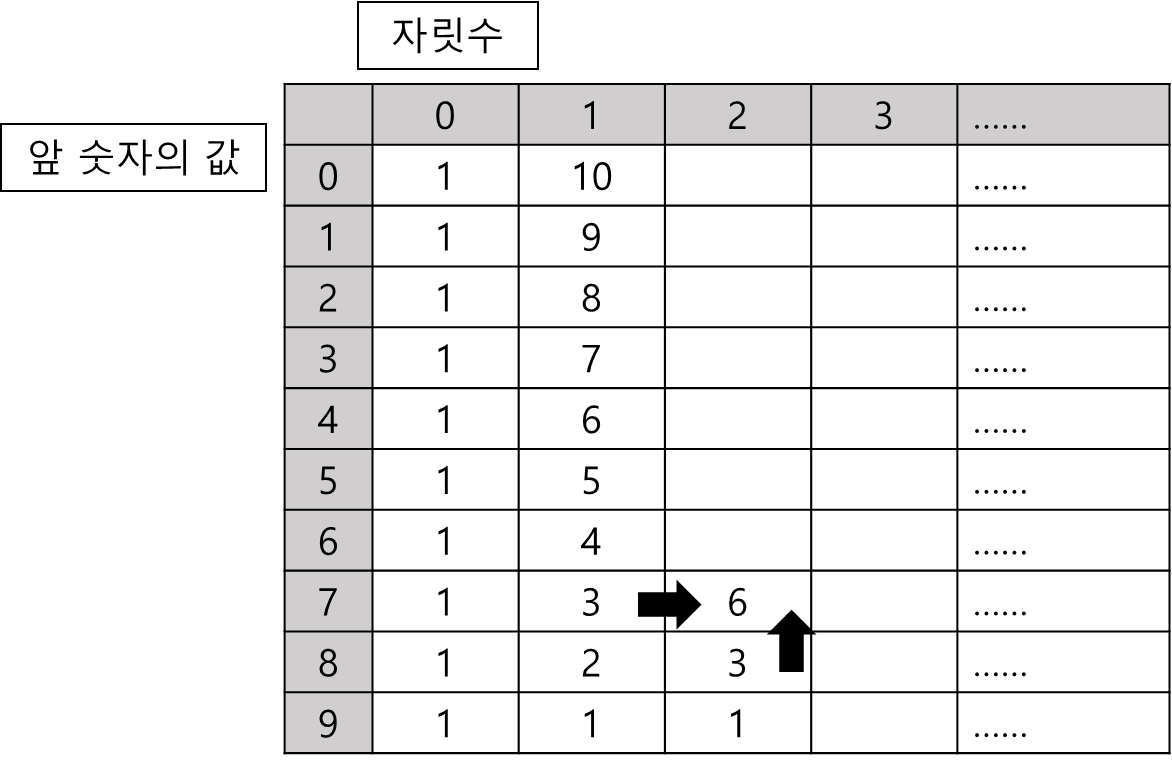
바로 느낌이 오지 않는다면, 아래의 7로 시작하는 3자리 오르막수의 개수를 계산하는 예시를 보자

이는 7로 시작하는 2자리 오르막수의 개수 + 8로 시작하는 3자리 오르막수의 개수로 표현이 가능하다

위의 규칙을 이해했다면 (혹은 자신만의 규칙을 찾았다면) 구현은 간단하다.
다만 위의 규칙을 이용할 것이라면 한 가지 다른 부분이 있다.
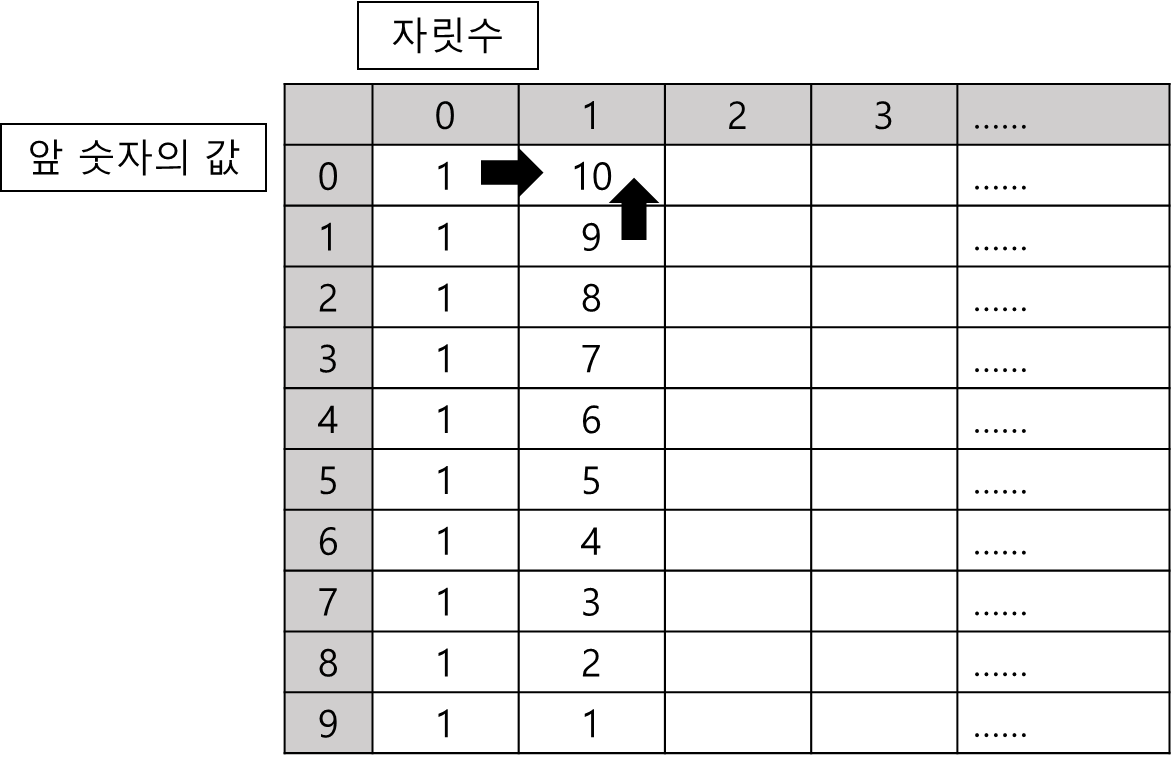
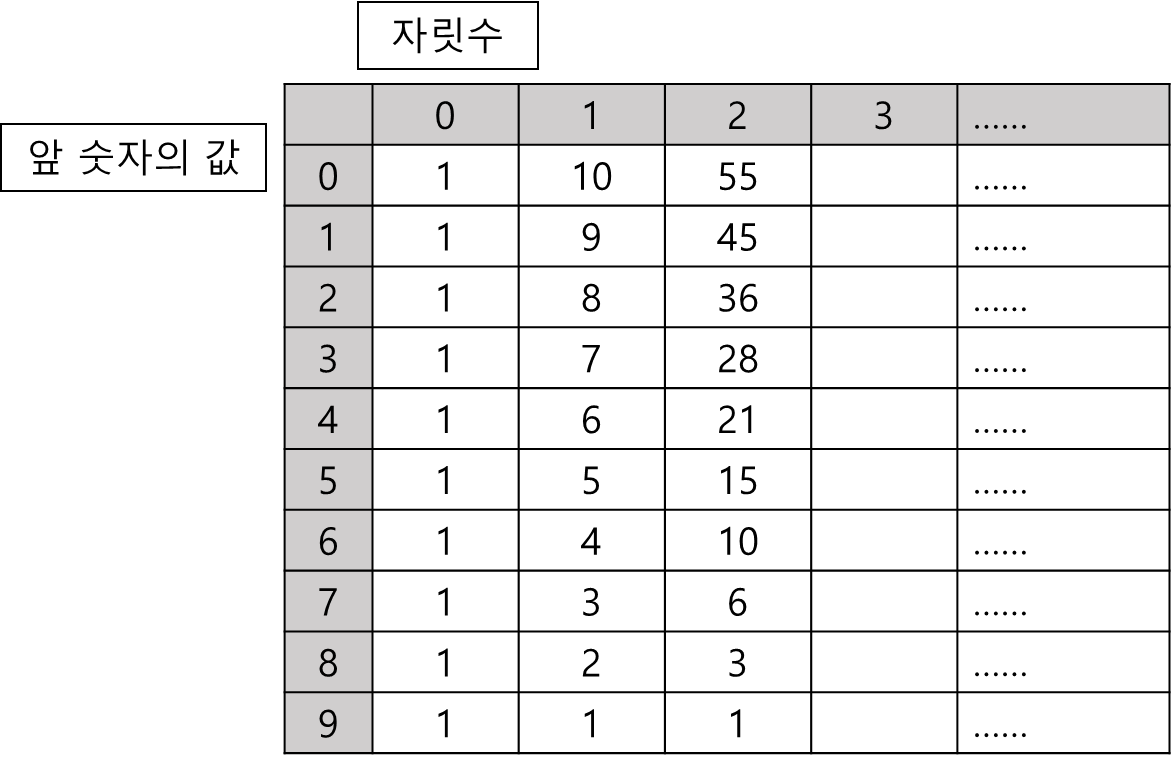
한자리 정수 S가 있을 때, S * 10^N 이상의, N+1 자릿수의 양수 중 오르막 수의 개수를 sum(S, N)이라 표현한다면
sum(S, N) = sum(S+1, N) + sum(S, N-1)이다.
거의 유사하지만 누적된 값을 이용한다는 차이가 있다.


0 자릿수 값은 모두 1로 초기화해 준다.
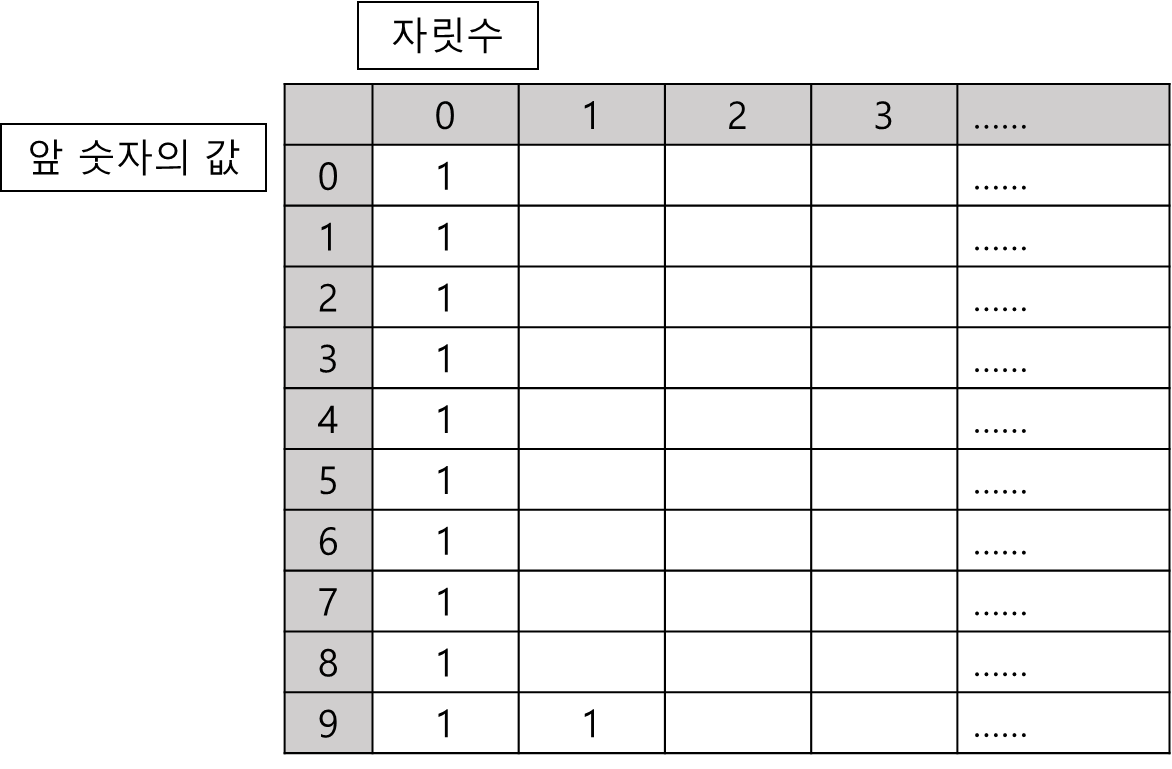
S가 9인 경우, sum(9, N)의 값은 항상 1이다.





code
GitHub - YoungWoo93/algorithmOnlineJudge: 알고리즘 온라인 저지
알고리즘 온라인 저지. Contribute to YoungWoo93/algorithmOnlineJudge development by creating an account on GitHub.
github.com
'알고리즘 온라인 저지 > BOJ' 카테고리의 다른 글
| BOJ 2239번 스도쿠 (0) | 2022.06.24 |
|---|---|
| BOJ 15711번 환상의 짝꿍 (0) | 2022.05.17 |
| BOJ 1389번 케빈 베이컨의 6단계 법칙 (0) | 2022.05.12 |
| BOJ 7576 토마토 (0) | 2022.02.10 |
| BOJ 11054 가장 긴 바이토닉 부분 수열 (0) | 2022.02.10 |


