9527번: 1의 개수 세기
두 자연수 A, B가 주어졌을 때, A ≤ x ≤ B를 만족하는 모든 x에 대해 x를 이진수로 표현했을 때 1의 개수의 합을 구하는 프로그램을 작성하시오. 즉, f(x) = x를 이진수로 표현 했을 때 1의 개수라
www.acmicpc.net
이 문제는 이진수에 대한 이해와, DP를 잘 응용할 수 있는지를 묻는 문제라고 느꼈다.
동적 계획법, 또는 DP 에 대해 잘 모른다면 아래의 더보기 포스팅을 참고하자.
우선, 문제 해석을 먼저 하겠다.
문제는 입력받은 숫자 2개를 포함하며 사이에 있는 모든 숫자를 2진수로 표현했을 때, 그 표현들에 포함된 1의 개수의 총 합을 출력하는 문제이다.
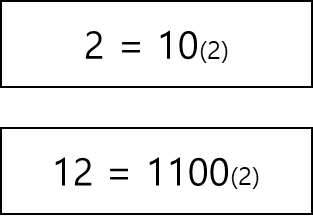
문제의 입력으로 주어진 2와 12를 이진수로 표현하면 위와 같다.
만약 10진수를 2진수로 바꾸지 못하겠다면, 문제를 풀기 앞서 진법 변환과 이진수에 대하여 학습해야 한다.
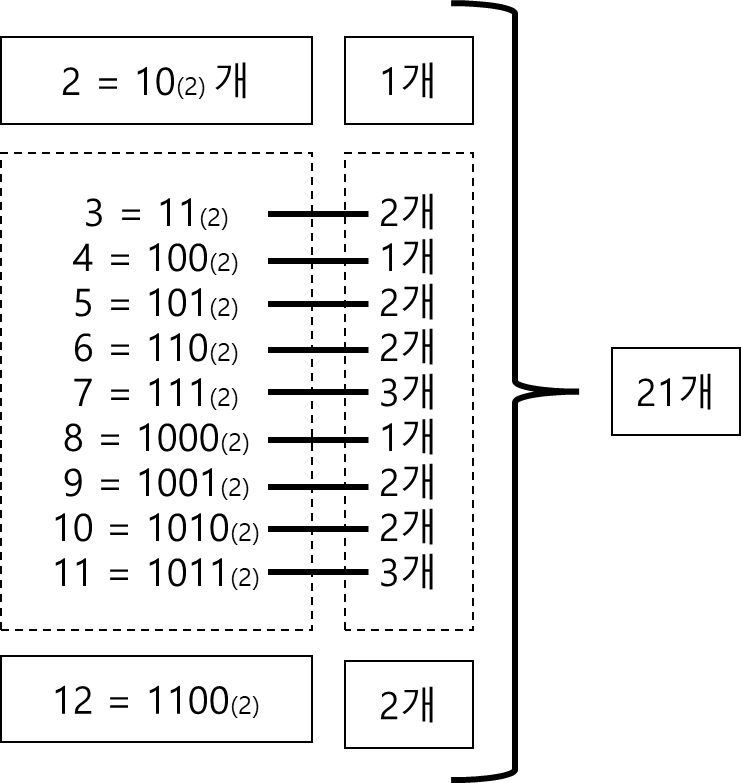
문제에서 요구하는 바는 위와 같다.
아마 이 문제를 풀기 위해 입력 사이의 모든 수를 반복문을 통해 이진수로 변환하고, 그 합을 구하는 형태로 진행했다면 대부분 시간 초과에 걸렸을 것이다. DP를 이용해 시간 초과를 극복해보자.

우선 1의 개수의 누적합을 가지는 DP 테이블이 있을 때, DP를 통해 문제의 답을 쉽게 구하는 방법을 설명한 뒤, 실제로 사용할 DP 테이블을 만들어본다.
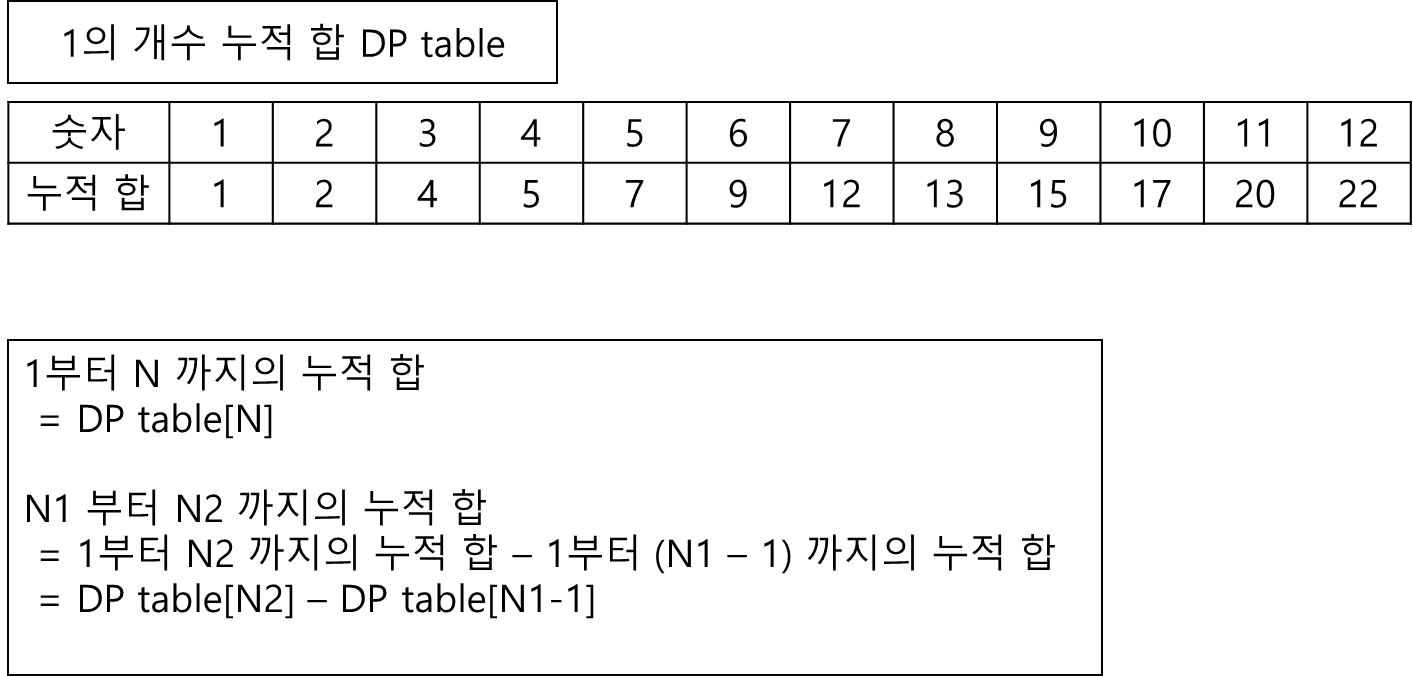
1부터 시작한, 누적 합을 구한 DP 테이블이 있다면, 당연히 1부터 N까지의 누적합은 table [N]의 값에 저장이 될 것이다.
그렇다면 N1부터 N2의 누적합은 어떻게 계산할 수 있을까?
그것은 table [N2] - table [N1 - 1]로 구할 수 있다, 만약 N1을 제외한다면 table [N2] - table [N1] 이 된다.
한 번에 느낌이 안 올 수 있다. 하지만 종이에 그림을 그려보면 당연하다는 것을 알 수 있다.

N1을 3, N2를 12라고 가정하자. 그렇다면 원하는 값을 위 그림의 검은 막대로 표현할 수 있다.
검은 막대는 파란 막대에서 빨간 막대를 뺀 크기이다.
파란 막대는 1부터 12 (= N2)까지의 크기이고
빨간 막대는 1부터 2 (= N1 - 1)까지의 크기이다.
즉 검은 막대 = 파란 막대 - 빨간 막대 가 되고
N1부터 N2까지의 누적합 = 1부터 N2까지의 누적합 - 1부터 (N1 - 1)까지의 누적합 이 된다.
즉 문제의 예시인 2 ~ 12 사이의 1의 개수는, 1의 갯수 누적합 DP 테이블을 구한 뒤 table [12] - table [1]을 한 값이 정답이 된다.
이제 DP 테이블이 있다면 문제의 답을 구할 수 있게 되었다. 그렇다면 그 DP 테이블은 어떻게 만들어야 할까?

두 가지 방법을 제시할 예정이지만, 그에 앞서 방법 설명에 이용할 오른쪽 표에 대하여 이야기하겠다.
이 표는 정수 N을 이진수로 나타낸 것을 보여준다.
가장 왼쪽의 값은 정수 N을 나타내면 그 이후로 이진수로 변환한 5비트 값을 나타낸다.
즉 6번째 줄의 값은
"정수 5를 이진수로 변환하면 00101이다."라는 의미이다.
우선 첫 번째 방법으로 이진수의 특성을 이용하는 방법이다. 임의로 세로 패턴이라고 불러본다.

세로 패턴을 이용할 경우, 임의의 N을 2로 나누었을 때, 그 몫은 01 이 반복되는 패턴의 개수가 된다.
반복되는 패턴마다 1이 1개씩 있다는 점을 이용하자.
같은 방법으로 N을 4로 나누었을 때, 그 몫은 0011이 반복되는 패턴의 개수와 같다. 패턴마다 1이 2개씩 있다.
하지만 노란색 세로줄과 다르게 나머지의 영역에 1이 존재할 수 있다. (= 00 11 패턴이 완성되지는 않았지만 00 1까지 오게 되어 1이 한 개 존재할 경우)
그러므로 초록 세로줄 이후로는 나머지에 대한 처리가 필요하다.
위의 이진수 특징을 이용한 방법도 틀린 방법은 아니지만, 문제에서 입력되는 범위가 매우 크기 때문에 맨 밑의 코드는 이번에 설명할 블록단위 패턴을 이용했다.

한눈에 파란 블록, 초록 블록, 빨간 블록의 관계를 이해하기 힘들지만 천천히 계산해보면 일정한 규칙이 있음을 알 수 있다.
특히 빨간 블록을 생각해내기 어려웠다. 빨간 블록에 대한 예시를 보자.

13까지의 1의 개수 누적합을 구하려 하는 예시를 설정해보았다.
여기서 8~13 영역을 차지하는 빨간 블록과 0~5 영역을 차지하는 빨간 블록의 구성이 동일함을 알 수 있다. 이 블록들의 규칙은 더 큰 값에서도 일정하게 반복된다.
제시한 두 가지 규칙은 직접 문제를 풀면서 떠올린 방식이기 때문에 더 효율적인 방법이 많을 것이다. 이러한 유형의 문제를 푸는 정석이 따로 존재할 수 있다.
이 문제를 포스팅한 목적 자체는 동적 계획법 자체가 하나의 틀이 아닌, 어디에도 응용 가능한 테크닉이라는 느낌을 전달하고 싶었기 때문에, 100점짜리 해설이 아니라는 것을 감안해서 이해했으면 좋겠다.
code
GitHub - YoungWoo93/algorithmOnlineJudge: 알고리즘 온라인 저지
알고리즘 온라인 저지. Contribute to YoungWoo93/algorithmOnlineJudge development by creating an account on GitHub.
github.com
'알고리즘 온라인 저지 > BOJ' 카테고리의 다른 글
| BOJ 10815번 숫자 카드 (0) | 2022.08.15 |
|---|---|
| BOJ 5430번 AC (0) | 2022.08.15 |
| BOJ 2294번 동전 2 (0) | 2022.08.10 |
| BOJ 7579번 앱 (0) | 2022.06.24 |
| BOJ 2239번 스도쿠 (0) | 2022.06.24 |

