1931번: 회의실 배정
(1,4), (5,7), (8,11), (12,14) 를 이용할 수 있다.
www.acmicpc.net
회의실에서 소화 가능한 회의의 개수의 최댓값을 묻는 문제이다. 회의 시간이 아닌 회의 개수 이므로 임의의 시점에서 회의실에 들어갈 수 있는 회의 중 가장 빨리 끝나는 회의를 탐욕적으로 선택하면 끝.
심지어 회의 번호를 기억할 필요도 없이 단순 횟수만 출력하면 되기 때문에 비교적 간단하게 구현할 수 있다.
위의 BOJ 예시를 그래프로 나타내면 아래와 같다.
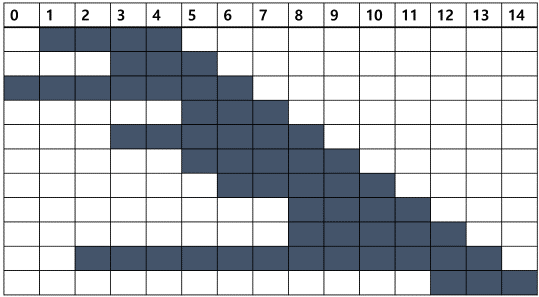
이 그래프를 이용하여 설명을 진행한다.
몇 가지 규칙을 정하고 그 규칙 대로만 (=알고리즘) 이 문제를 해결하기로 한다.
- (규칙 A) 현재시간 커서 이후에 시작 예정인 회의 중 가장 빠르게 종료 예정인 회의를 회의실에 투입한다.
- (규칙 B) 현재시간 커서를 방금 투입했던 회의의 종료시간으로 옮긴 후 규칙 A로 돌아간다.
규칙은 간단하다.
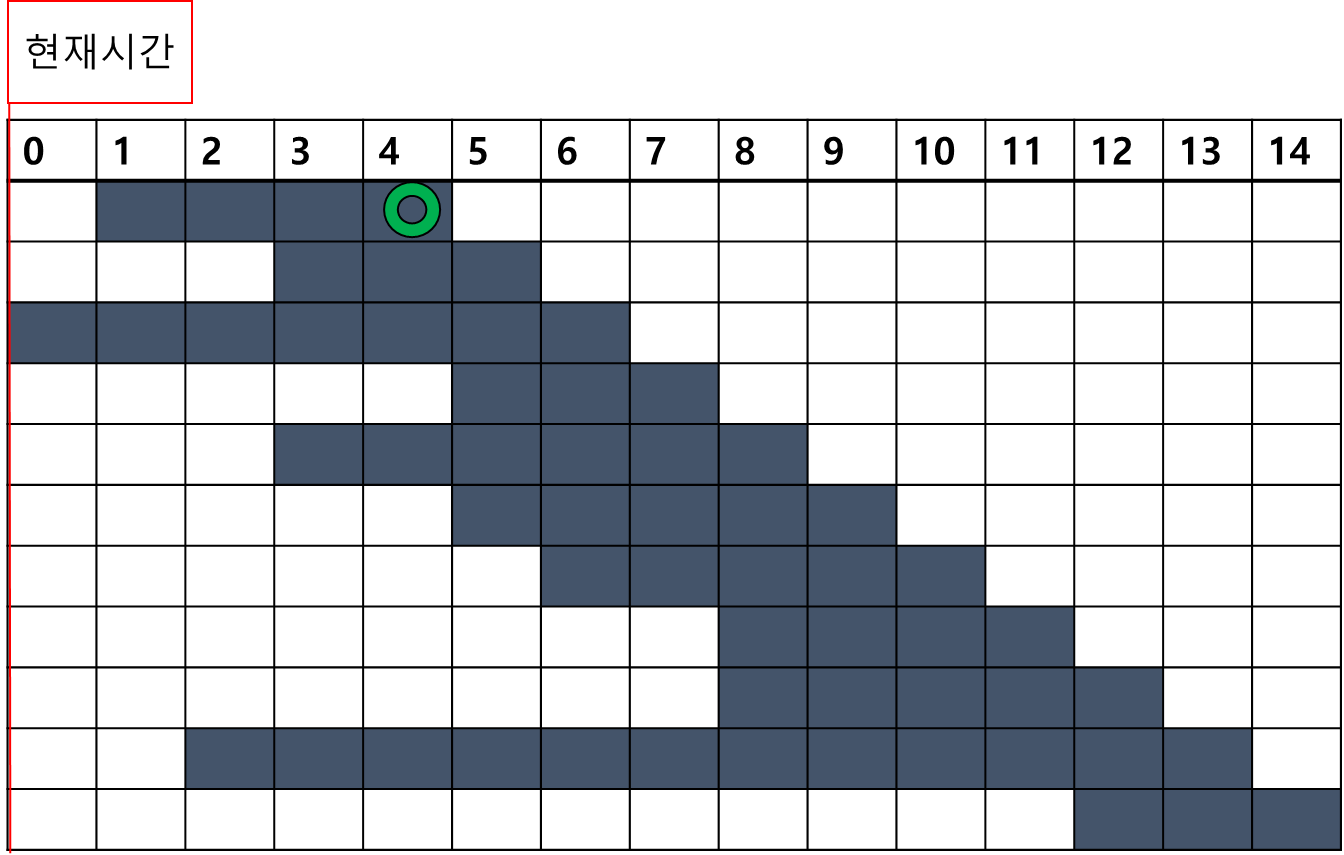
바로 첫 번째 회의 (시작시간 기준이 아닌 종료시간 기준 첫 번째 회의 임에 유의)는 바로 투입이 가능하다.


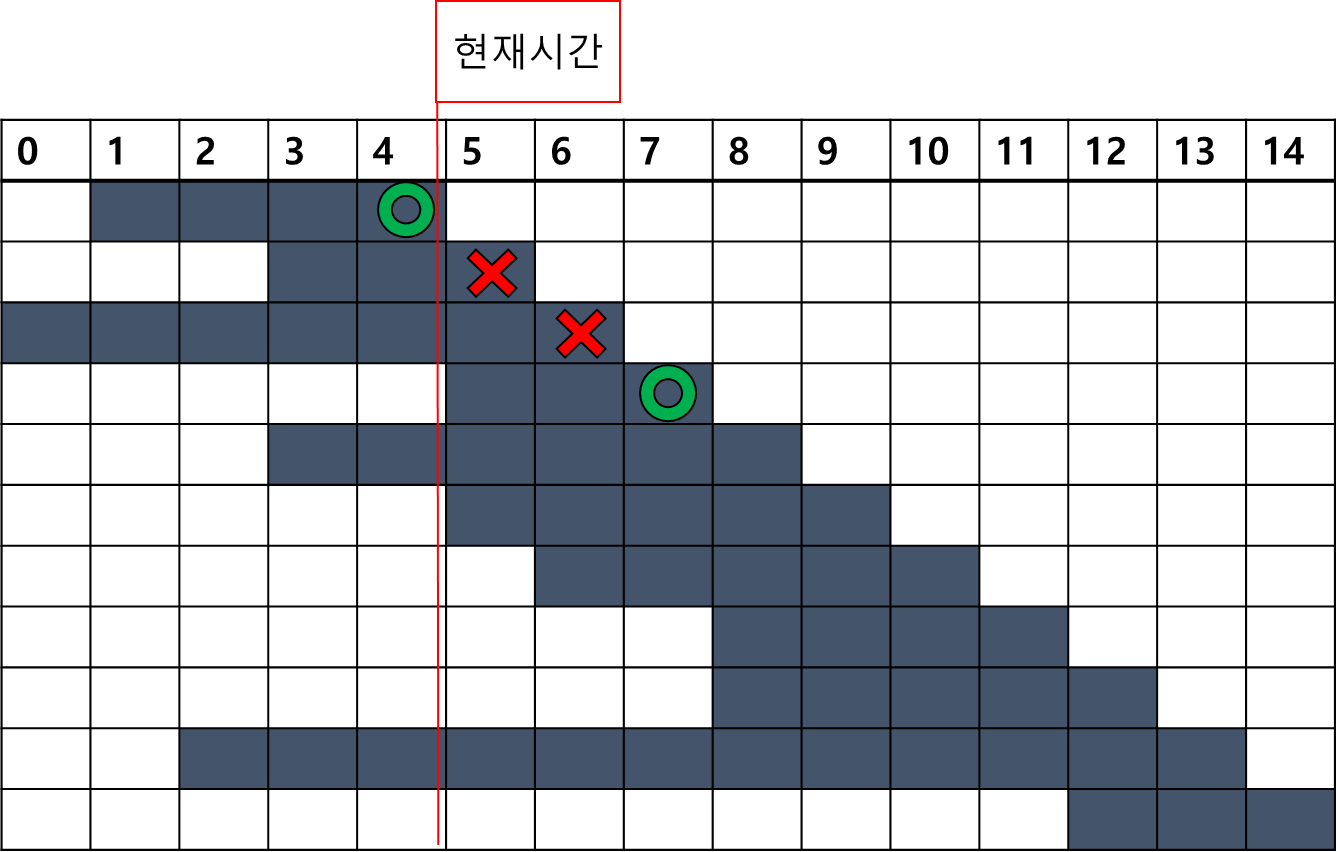
두 번째 회의 선택부터 현재시간이 증가함에 따라 투입이 불가능한 회의들이 있다. 이것들만 한번 걸러주면 간단하게 정답이 나온다.
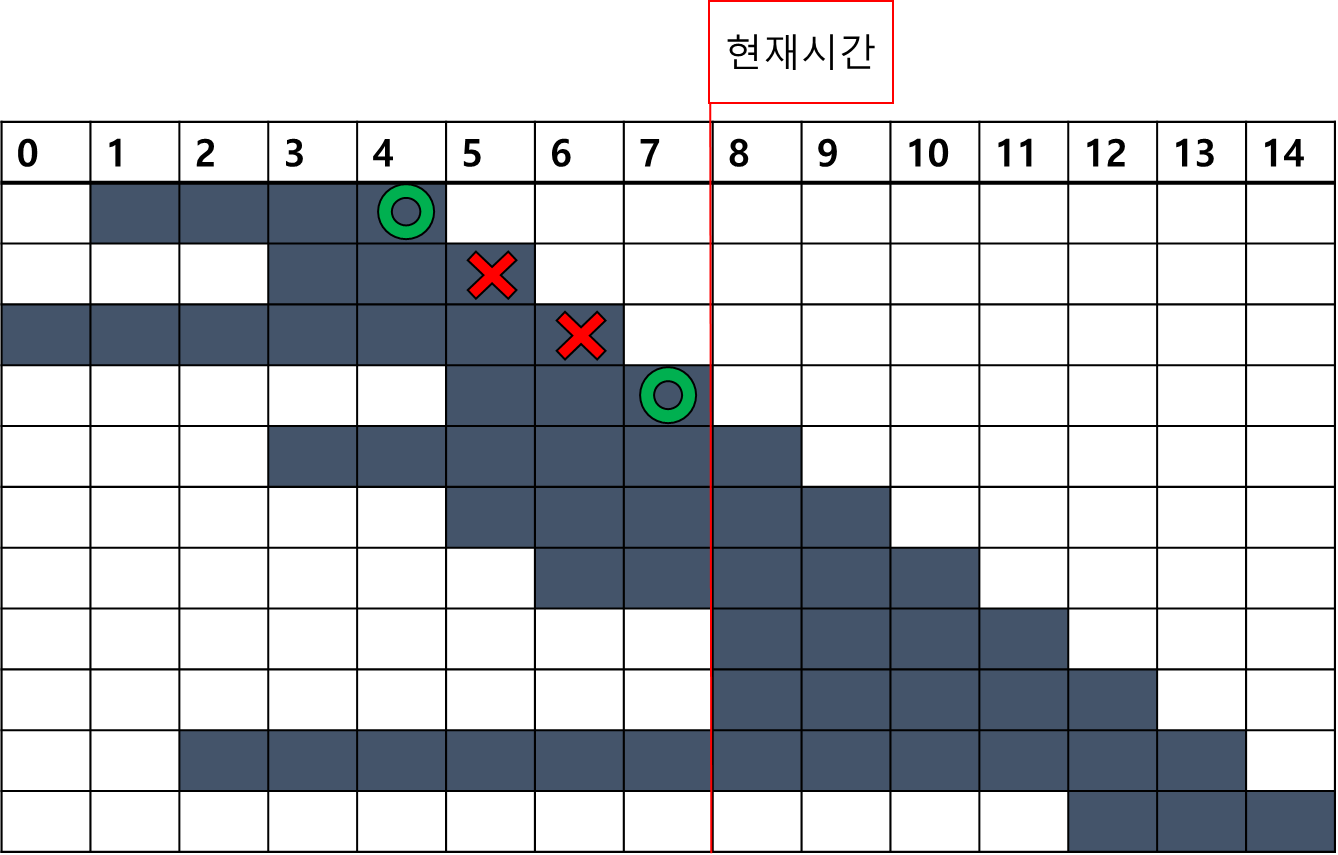
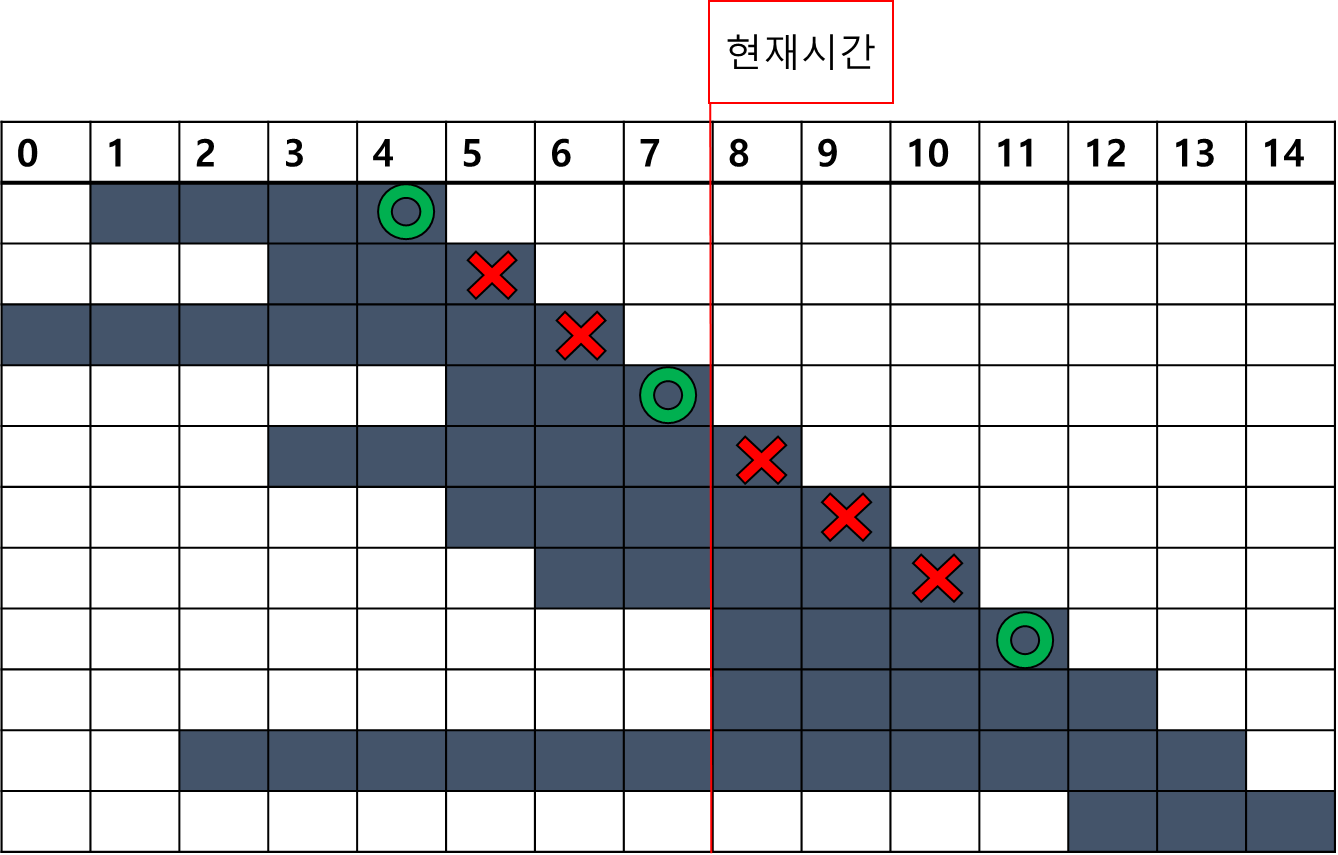

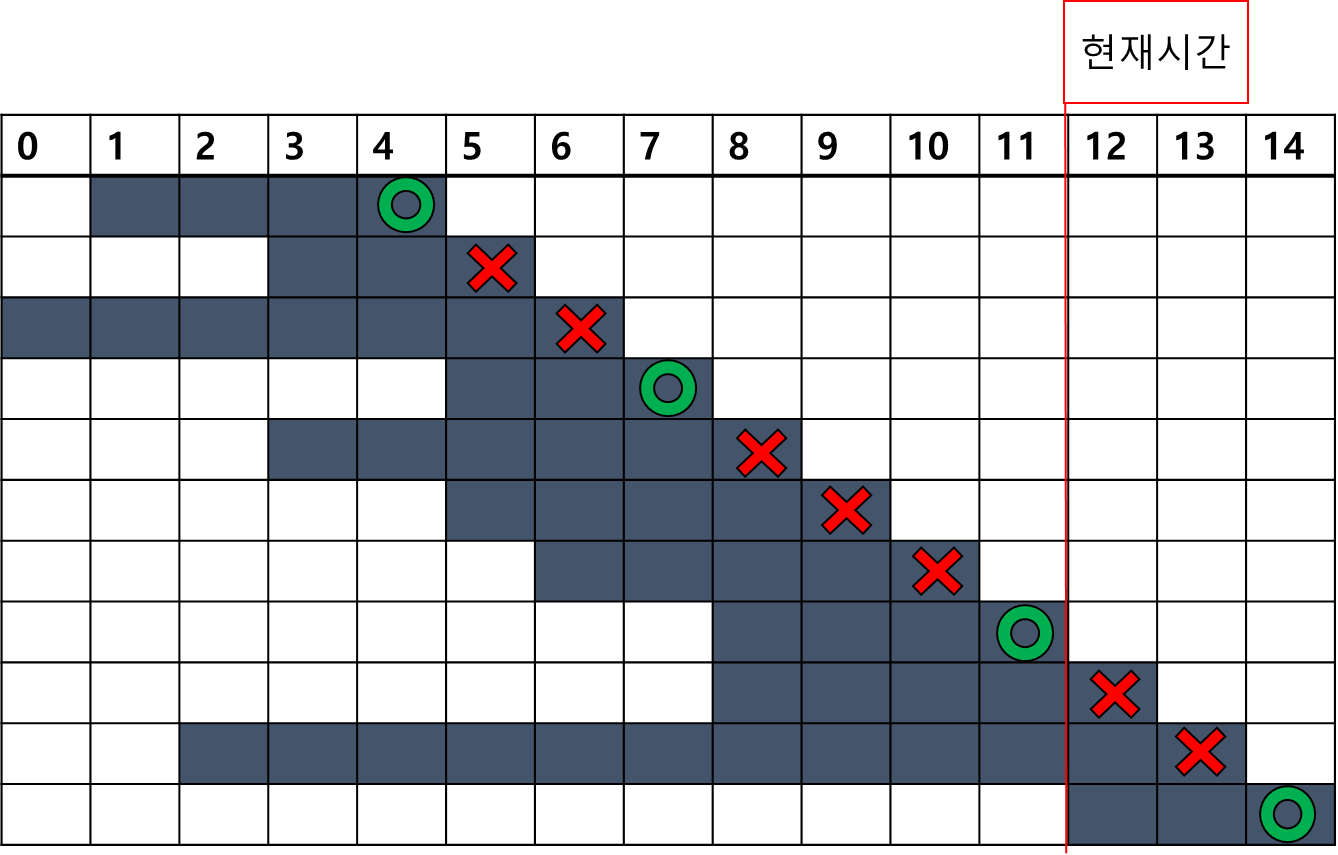
그래프가 아주 간단하게 나왔지만 사실 이렇게 간단하게 설명한 것 에는 한 가지 전제조건이 있다.
모든 회의가 종료시간 기준으로 오름차순 정렬이 되어 있어야 한다는 점이다.
만약 다음과 같이 정렬이 되지 않은 시간을 회의 시간을 그래프로 나타냈다면
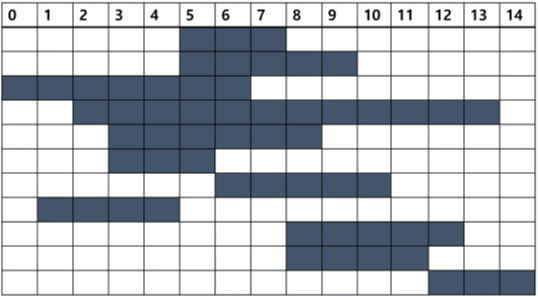

모든 회의가 투입 가능해지고, 이들 중 가장 빨리 끝나는 회의를 추가로 찾아야 할 뿐만 아니라.

중간 단계에서도 모든 회의에 대하여 불가능 판정을 새로 내려야 하기 때문에 프로그램이 계산해야 할 양 자체가 N^2 배로 많아진다.
즉 시간 초과 처리가 될 가능성이 매우 높아지는 것이다.
물론 정렬을 했다고 해서 무조건 시간 복잡도가 빠르게 나오는 것 은 아니다. 정렬을 한 뒤에도 전체 탐색을 한다면 똑같이 시간 복잡도가 크게 나온다.
(규칙 A) 현재시간 커서 이후에 시작 예정인 회의 중 가장 빠르게 종료 예정인 회의를 회의실에 투입한다.
포인트는 탐색을 하는 커서를 현재 시간 이전에 대해서 하지 않는 것에 있다.
code
GitHub - YoungWoo93/algorithmOnlineJudge: 알고리즘 온라인 저지
알고리즘 온라인 저지. Contribute to YoungWoo93/algorithmOnlineJudge development by creating an account on GitHub.
github.com
'알고리즘 온라인 저지 > BOJ' 카테고리의 다른 글
| BOJ 1644 소수의 연속합 (0) | 2022.01.10 |
|---|---|
| BOJ 4948 베르트랑 공준 (0) | 2022.01.10 |
| BOJ 1715번 카드 정렬하기 (0) | 2022.01.09 |
| BOJ 1005번 ACM Craft (0) | 2022.01.08 |
| BOJ 5638번 수문 (0) | 2022.01.08 |


