2178번: 미로 탐색
첫째 줄에 두 정수 N, M(2 ≤ N, M ≤ 100)이 주어진다. 다음 N개의 줄에는 M개의 정수로 미로가 주어진다. 각각의 수들은 붙어서 입력으로 주어진다.
www.acmicpc.net
미로 찾기 문제이지만 최단거리를 구해야 하므로 가장 간단한 BFS를 이용하여 푼 문제이다.
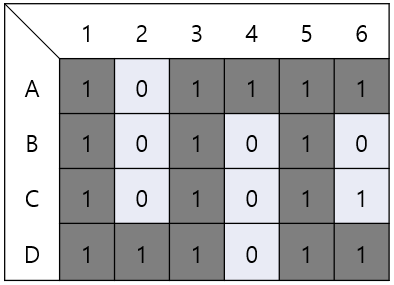
오른쪽과 같이 문제에서 제시된 미로를 이용하며.
큐를 이용한 BFS를 이용하여 간단하게 문제를 풀고자 한다.
이때 일반적인 미로 찾기 입문 문제처럼 스택을 이용하지는 않는다. 그 이유는 스택을 이용할 경우 미로 최단경로를 찾기 위해서는 휴리스틱을 추가로 사용해야 하기 때문에 내용이 많아지기 때문이다.
휴리스틱을 위한 포스팅은 이후에 따로 하도록 하겠다.

위의 미로 지도와, 큐, 들어갈 노드를 이용해서 이 문제를 풀어보자.
규칙은 다음과 같다.
- (규칙 A) 큐에서 노드를 하나 꺼내고, 해당 노드(칸)에서 상하좌우로 이동 가능한 위치가 있다면 큐에 새롭게 넣어준다.
- (규칙 A-1) 이때, 이동 가능하더라도 이미 이동한 적이 있는 위치의 경우 새롭게 큐에 넣지 않는다.
- (규칙 B) 큐가 완전히 비거나 (도달 불가능) / 목적지에 도착할 때까지 (규칙 A)를 반복한다.
매우 간단한 규칙이며, 문제의 해결을 위해 2가지 조건을 더 추가한다.
1. 큐에 노드를 넣는 시점에서 지도상 해당 위치를 이동 불가 지역으로 만든다. (규칙 A-1을 위함)
2. 큐에 노드를 넣는 시점에서, 직전 단계까지의 걸음 수 + 1의 값을 노드에 추가로 저장시킨다. (최소 거리 값을 알기 위함)
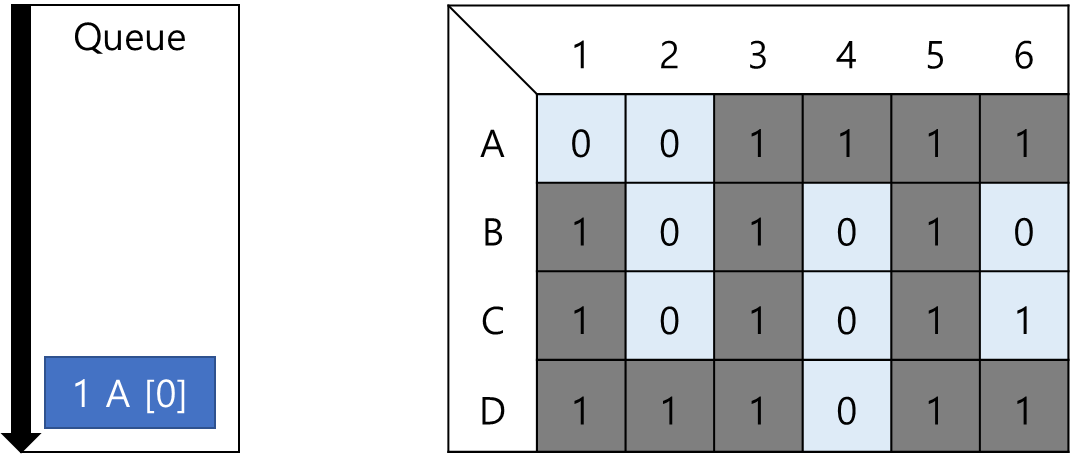
최초에 1,A 값을 넣어주며 시작한다, 이때 거리를 대괄호로 묶어 표현한다.

규칙 A 에 의해 큐에서 노드를 하나 꺼내고, 이동 가능한 위치가 있는지 확인한다.
1, B 가 이동 가능한 위치임을 확인할 수 있다.
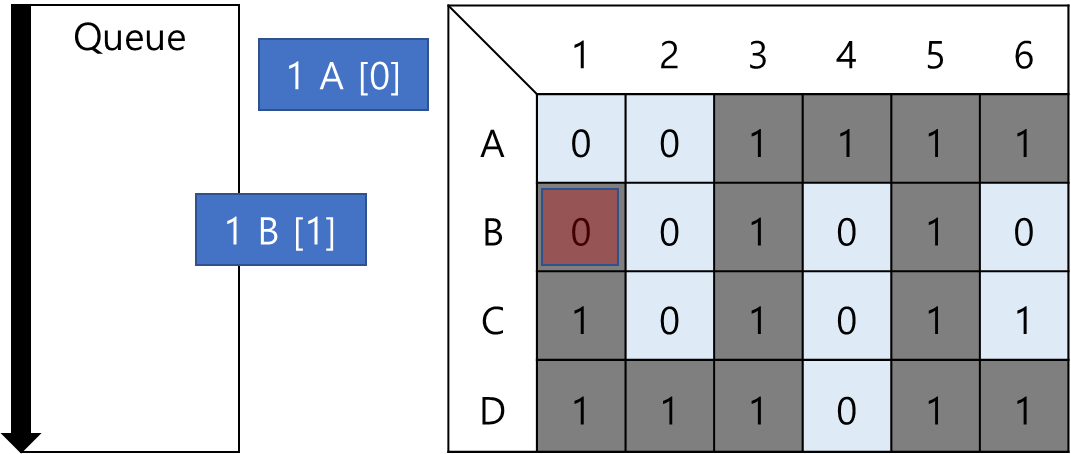
큐에 1, B를 넣어줄 때, 기존의 걸음수인 0에서 1을 더한 값을 같이 넣어 큐에 저장한다. 또한 중복을 방지하기 위하여 새로 넣어지는 좌표 칸의 값을 이동 불가능하게 (= 0으로) 바꾸어준다.
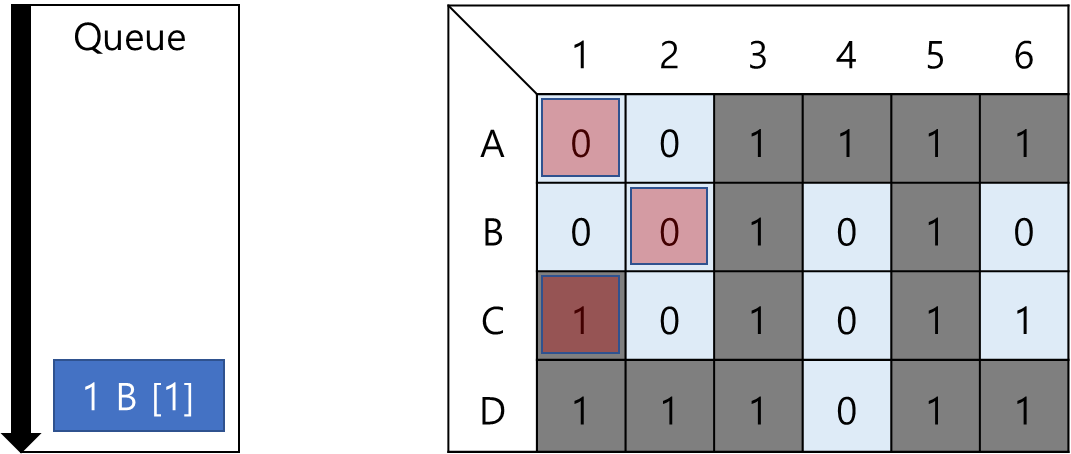
이대로 규칙 A를 반복하면 된다.
그렇게 규칙 A를 반복하다 보면
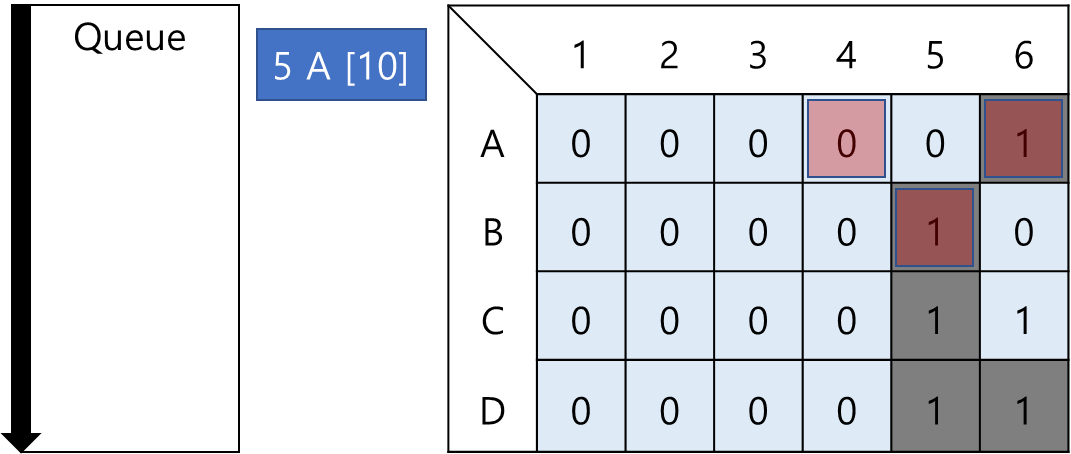
5, A 지점까지 오게된다. 여기서는 길이 두 갈래로 나뉘기 때문에 (6, A, [11]), (5, B, [11]) 두 개의 노드가 큐에 들어가게 된다.
물론 (6, A, [11])에서 더 이상 이동 가능한 공간이 없기 때문에 자연스럽게 삭제가 되며 목적지인 6, D로 이동하여 14라는 거리를 얻을 수 있다.
포스팅을 올린 뒤, 거리가 아니라 칸 수를 얻어야 하는 문제였음을 깨닳았다. 칸 수는 거리 +1 이므로 계산 결과에 +1을 해주면 된다...
큐를 이용한 간단한 BFS를 구현했으며
2차원 행렬을 이용한 BFS와, DFS 가 남았다.
code
GitHub - YoungWoo93/algorithmOnlineJudge: 알고리즘 온라인 저지
알고리즘 온라인 저지. Contribute to YoungWoo93/algorithmOnlineJudge development by creating an account on GitHub.
github.com
'알고리즘 온라인 저지 > BOJ' 카테고리의 다른 글
| BOJ 1463 1로 만들기 (0) | 2022.01.30 |
|---|---|
| BOJ 1339 단어 수학 (0) | 2022.01.30 |
| BOJ 1238 파티 (0) | 2022.01.28 |
| BOJ 1202번 보석 도둑 (0) | 2022.01.18 |
| BOJ 2014 소수의 곱 (0) | 2022.01.18 |


